
【題目】已知橢圓![]() 的中心在坐標原點,焦點在坐標軸上,且經(jīng)過
的中心在坐標原點,焦點在坐標軸上,且經(jīng)過![]() 、
、![]() 、
、![]() 三點.
三點.
(1)求橢圓![]() 的方程;
的方程;
(2)若直線![]() :
:![]() (
(![]() )與橢圓
)與橢圓![]() 交于
交于![]() 、
、![]() 兩點,證明直線
兩點,證明直線![]() 與直線
與直線![]() 的交點在直線
的交點在直線![]() 上.
上.
【答案】(1)![]() ;(2)詳見解析.
;(2)詳見解析.
【解析】
試題(1)當焦點不確定在哪個軸時,可以分別討論在![]() 軸時,
軸時,![]() ,代入
,代入![]() 點,當在
點,當在![]() 軸時
軸時![]() ,代入
,代入![]() 點解
點解![]() 或
或![]() ,成立的就是橢圓方程;或直接設橢圓的一般式
,成立的就是橢圓方程;或直接設橢圓的一般式![]() ,代入三點的坐標解方程組;
,代入三點的坐標解方程組;
(2)直線方程![]() 與橢圓方程聯(lián)立,設
與橢圓方程聯(lián)立,設![]() ,
,![]() ,由根與系數(shù)的關系得到
,由根與系數(shù)的關系得到![]() 和
和![]() 設直線
設直線![]() 的方程
的方程![]() ,直線
,直線![]() 的方程為
的方程為![]() 后有三種方法,法一,當
后有三種方法,法一,當![]() 時計算交點的縱坐標,并根據(jù)直線方程與根與系數(shù)的關系證明縱坐標相等,法二是聯(lián)立直線
時計算交點的縱坐標,并根據(jù)直線方程與根與系數(shù)的關系證明縱坐標相等,法二是聯(lián)立直線![]() 與
與![]() 的方程,消去
的方程,消去![]() 后利用根與系數(shù)的關系得到交點的橫坐標等于4,法三類似于法二,只是先通過根與系數(shù)的關系先消去
后利用根與系數(shù)的關系得到交點的橫坐標等于4,法三類似于法二,只是先通過根與系數(shù)的關系先消去![]() ,得到
,得到![]() 與
與![]() 的關系,然后再聯(lián)立兩個方程得到交點橫坐標為4.
的關系,然后再聯(lián)立兩個方程得到交點橫坐標為4.
試題解析:(1)解法一:當橢圓E的焦點在x軸上時,設其方程為![]() (
(![]() ),
),
則![]() ,又點
,又點![]() 在橢圓
在橢圓![]() 上,得
上,得![]() .解得
.解得![]() .
.
∴橢圓![]() 的方程為
的方程為![]() .
.
當橢圓E的焦點在y軸上時,設其方程為![]() (
(![]() ),
),
則![]() ,又點
,又點![]() 在橢圓
在橢圓![]() 上,得
上,得![]() .
.
解得![]() ,這與
,這與![]() 矛盾.
矛盾.
綜上可知,橢圓![]() 的方程為
的方程為![]() .
.
解法二:設橢圓方程為![]() (
(![]() ),
),
將![]() 、
、![]() 、
、![]() 代入橢圓
代入橢圓![]() 的方程,得
的方程,得
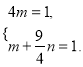 解得
解得![]() ,
,![]() .
.
∴橢圓![]() 的方程為
的方程為![]() .
.
(2)證法一:將直線![]() :
:![]() 代入橢圓
代入橢圓![]() 的方程
的方程![]() 并整理,得
并整理,得![]() ,
,
設直線![]() 與橢圓
與橢圓![]() 的交點
的交點![]() ,
,![]() ,
,
由根與系數(shù)的關系,得![]() ,
,![]() .
.
直線![]() 的方程為:
的方程為:![]() ,它與直線
,它與直線![]() 的交點坐標為
的交點坐標為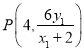 ,
,
同理可求得直線![]() 與直線
與直線![]() 的交點坐標為
的交點坐標為 .
.
下面證明![]() 、
、![]() 兩點重合,即證明
兩點重合,即證明![]() 、
、![]() 兩點的縱坐標相等:
兩點的縱坐標相等:
∵![]() ,
,![]() ,
,
∴![]()
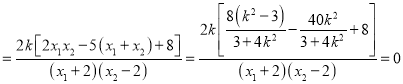 .
.
因此結論成立.
綜上可知,直線![]() 與直線
與直線![]() 的交點在直線
的交點在直線![]() 上.
上.
證法二:將直線![]() :
:![]() ,代入橢圓
,代入橢圓![]() 的方程
的方程![]() 并整理,
并整理,
得![]() ,
,
設直線![]() 與橢圓
與橢圓![]() 的交點
的交點![]() ,
,![]() ,
,
由根與系數(shù)的關系,得![]() ,
,![]() .
.
直線![]() 的方程為:
的方程為:![]() ,即
,即![]() .
.
直線![]() 的方程為:
的方程為:![]() ,即
,即![]() .
.
由直線![]() 與直線
與直線![]() 的方程消去
的方程消去![]() ,得
,得
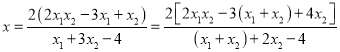
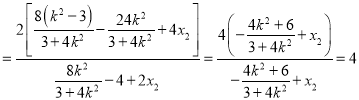 .
.
∴直線![]() 與直線
與直線![]() 的交點在直線
的交點在直線![]() 上.
上.
證法三:將直線![]() :
:![]() ,代入橢圓方程
,代入橢圓方程![]() 并整理,
并整理,
得![]() ,
,
設直線![]() 與橢圓
與橢圓![]() 的交點
的交點![]() ,
,![]() ,
,
由根與系數(shù)的關系,得![]() ,
,![]() .
.
消去![]() 得,
得,![]() .
.
直線![]() 的方程為:
的方程為:![]() ,即
,即![]() .
.
直線![]() 的方程為:
的方程為:![]() ,即
,即![]() .
.
由直線![]() 與直線
與直線![]() 的方程消去
的方程消去![]() 得,
得,
 .
.
∴直線![]() 與直線
與直線![]() 的交點在直線
的交點在直線![]() 上.
上.


科目:高中數(shù)學 來源: 題型:
【題目】設函數(shù)![]()
(1)當a=b=1時,求函數(shù)f(x)的圖象在點(e2,f(e2))處的切線方程;
(2)當b=1時,若存在![]() ,使f(x1)≤f'(x2)+a成立,求實數(shù)a的最小值.
,使f(x1)≤f'(x2)+a成立,求實數(shù)a的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知雙曲線C:![]() ,O為坐標原點,F為C的右焦點,過F的直線與C的兩條漸近線的交點分別為M、N.若
,O為坐標原點,F為C的右焦點,過F的直線與C的兩條漸近線的交點分別為M、N.若![]() OMN為直角三角形,則|MN|=
OMN為直角三角形,則|MN|=
A. ![]() B. 3 C.
B. 3 C. ![]() D. 4
D. 4
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知過拋物線C:y2=8x的焦點且斜率為k的直線與C交于A、B兩點,若以AB為直徑的圓過點M(﹣2,2),則k=( )
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】2018年9月24日,阿貝爾獎和菲爾茲獎雙料得主、英國著名數(shù)學家阿蒂亞爵士宣布自己證明了黎曼猜想,這一事件引起了數(shù)學界的震動.在1859年,德國數(shù)學家黎曼向科學院提交了題目為《論小于某值的素數(shù)個數(shù)》的論文并提出了一個命題,也就是著名的黎曼猜想.在此之前,著名數(shù)學家歐拉也曾研究過這個問題,并得到小于數(shù)字![]() 的素數(shù)個數(shù)大約可以表示為
的素數(shù)個數(shù)大約可以表示為![]() 的結論.若根據(jù)歐拉得出的結論,估計10000以內的素數(shù)的個數(shù)為(素數(shù)即質數(shù),
的結論.若根據(jù)歐拉得出的結論,估計10000以內的素數(shù)的個數(shù)為(素數(shù)即質數(shù),![]() ,計算結果取整數(shù))
,計算結果取整數(shù))
A. 1089 B. 1086 C. 434 D. 145
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在四邊形![]() 中,
中,![]() ,
,![]() ,點
,點![]() 在
在![]() 上,且
上,且![]() ,
,![]() ,現(xiàn)將
,現(xiàn)將![]() 沿
沿![]() 折起,使點
折起,使點![]() 到達點
到達點![]() 的位置,且
的位置,且![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,
,
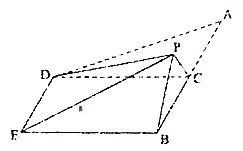
(1)求證:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設不等式組![]() 表示的區(qū)域為A,不等式組
表示的區(qū)域為A,不等式組![]() 表示的區(qū)域為B.
表示的區(qū)域為B.
(1)在區(qū)域A中任取一點(x,y),求點(x,y)∈B的概率;
(2)若x、y分別表示甲、乙兩人各擲一次骰子所得的點數(shù),求點(x,y)在區(qū)域B中的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知直線![]() ,
,![]() ,過點
,過點![]() 的直線
的直線![]() 分別與直線
分別與直線![]() ,
,![]() 交于
交于![]() ,其中點
,其中點![]() 在第三象限,點
在第三象限,點![]() 在第二象限,點
在第二象限,點![]() ;
;
(1)若![]() 的面積為
的面積為![]() ,求直線
,求直線![]() 的方程;
的方程;
(2)直線![]() 交于
交于![]() 點
點![]() ,直線
,直線![]() 交
交![]() 于點
于點![]() ,若
,若![]() 直線的斜率均存在,分別設為
直線的斜率均存在,分別設為![]() ,判斷
,判斷![]() 是否為定值?若為定值,求出該定值;若不為定值,說明理由.
是否為定值?若為定值,求出該定值;若不為定值,說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知非零數(shù)列![]() 的遞推公式為
的遞推公式為![]() ,
,![]() .
.
(1)求證數(shù)列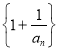 是等比數(shù)列;
是等比數(shù)列;
(2)若關于![]() 的不等式
的不等式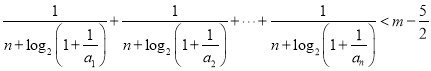 有解,求整數(shù)
有解,求整數(shù)![]() 的最小值;
的最小值;
(3)在數(shù)列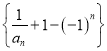 中,是否一定存在首項、第
中,是否一定存在首項、第![]() 項、第
項、第![]() 項
項![]() ,使得這三項依次成等差數(shù)列?若存在,請指出
,使得這三項依次成等差數(shù)列?若存在,請指出![]() 所滿足的條件;若不存在,請說明理由.
所滿足的條件;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com