
 ,使得對定義域
,使得對定義域 內(nèi)的任意兩個
內(nèi)的任意兩個 ,均有
,均有 成立,則稱函數(shù)
成立,則稱函數(shù) 在定義域
在定義域 上滿足利普希茨條件.若函數(shù)
上滿足利普希茨條件.若函數(shù) 滿足利普希茨條件,則常數(shù)
滿足利普希茨條件,則常數(shù) 的最小值為()
的最小值為()| A.4 | B.3 | C.1 | D.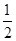 |
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
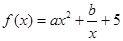
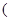 常數(shù)
常數(shù)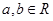 )滿足
)滿足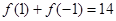 .
.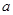 的值,并就常數(shù)
的值,并就常數(shù)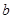 的不同取值討論函數(shù)
的不同取值討論函數(shù) 奇偶性;
奇偶性; 在區(qū)間
在區(qū)間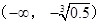 上單調(diào)遞減,求
上單調(diào)遞減,求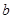 的最小值;
的最小值;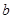 取最小值時,證明:
取最小值時,證明: 恰有一個零點
恰有一個零點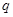 且存在遞增的正整數(shù)數(shù)列
且存在遞增的正整數(shù)數(shù)列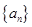 ,使得
,使得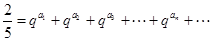 成立.
成立.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
 ,其中a為大于零的常數(shù).
,其中a為大于零的常數(shù). +
+ +…+
+…+ 恒成立.
恒成立. 查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題


查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
| A.﹣9 | B.﹣3 | C.9 | D.15 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
| A.(﹣∞,0) | B.(0,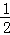 ) ) | C.(0,1) | D.(0,+∞) |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
 的定義域為R,若存在常數(shù)M>0,使
的定義域為R,若存在常數(shù)M>0,使 對 一切實數(shù)x均成 立,則稱
對 一切實數(shù)x均成 立,則稱 為“倍約束函數(shù)”,現(xiàn)給出下列函數(shù):①
為“倍約束函數(shù)”,現(xiàn)給出下列函數(shù):① :②
:②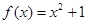 :③
:③ ;④
;④ ⑤
⑤ 是定義在實數(shù)集R上的奇函數(shù),且
是定義在實數(shù)集R上的奇函數(shù),且 均有
均有 ,其中是“倍約束函數(shù)”的有( )
,其中是“倍約束函數(shù)”的有( )| A.1個 | B.2個 | C.3個 | D.4個 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com