
【題目】如圖,正方體ABCD-A1B1C1D1的棱長為1,P為BC的中點(diǎn),Q為線段CC1上的動(dòng)點(diǎn),過點(diǎn)A,P,Q的平面截該正方體所得的截面記為S,則下列命題正確的是 .(填序號(hào))
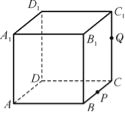
①當(dāng)0<CQ<![]() 時(shí),S為四邊形;
時(shí),S為四邊形;
②當(dāng)CQ=![]() 時(shí),S為等腰梯形;
時(shí),S為等腰梯形;
③當(dāng)CQ=![]() 時(shí),S與C1D1的交點(diǎn)R滿足C1R=
時(shí),S與C1D1的交點(diǎn)R滿足C1R=![]() ;
;
④當(dāng)![]() <CQ<1時(shí),S為六邊形;
<CQ<1時(shí),S為六邊形;
⑤當(dāng)CQ=1時(shí),S的面積為![]() .
.
【答案】①②③⑤
【解析】
試題分析:①正確,當(dāng)![]() 時(shí),截面S與正方體的另一個(gè)交點(diǎn)落在線段
時(shí),截面S與正方體的另一個(gè)交點(diǎn)落在線段![]() 上,所以截面為四邊形,②正確,當(dāng)
上,所以截面為四邊形,②正確,當(dāng)![]() 時(shí),截面S與正方體的另一個(gè)交點(diǎn)落在點(diǎn)
時(shí),截面S與正方體的另一個(gè)交點(diǎn)落在點(diǎn)![]() ,此時(shí)四邊形
,此時(shí)四邊形![]() 是等腰梯形,③正確,當(dāng)
是等腰梯形,③正確,當(dāng)![]() 時(shí),如圖延長
時(shí),如圖延長![]() 至
至![]() ,使
,使![]() ,連接AN交
,連接AN交![]() 于S,連接NQ交
于S,連接NQ交![]() 于R,連接SR,可證明
于R,連接SR,可證明![]() ,由
,由![]() ,可得
,可得![]() ,故可得
,故可得![]() ,所以正確;④當(dāng)
,所以正確;④當(dāng)![]() 時(shí),根據(jù)③可得四邊形是五邊形,不是六邊形,故不正確;⑤當(dāng)
時(shí),根據(jù)③可得四邊形是五邊形,不是六邊形,故不正確;⑤當(dāng)![]() 時(shí),
時(shí),
截面四邊形是邊長為![]() 的菱形,其對角線為正方形的對角線長
的菱形,其對角線為正方形的對角線長![]() ,另一條對角線長為面對角線長為
,另一條對角線長為面對角線長為![]() ,所以
,所以![]() ,故正確;故填:①②③⑤
,故正確;故填:①②③⑤




| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() ,
,![]() .
.
(1)求![]() 的極值;
的極值;
(2)設(shè)![]() ≤
≤![]() ,記
,記![]() 在
在![]() 上的最大值為
上的最大值為![]() ,求函數(shù)
,求函數(shù)![]() 的最小值;
的最小值;
(3)設(shè)函數(shù)![]() (
(![]() 為常數(shù)),若使
為常數(shù)),若使![]() ≤
≤![]() ≤
≤![]() 在
在![]() 上恒成立的實(shí)數(shù)
上恒成立的實(shí)數(shù)![]() 有且只有一個(gè),求實(shí)數(shù)
有且只有一個(gè),求實(shí)數(shù)![]() 和
和![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 是矩形,
是矩形,![]() ,
,![]() 是
是![]() 的中點(diǎn).
的中點(diǎn).
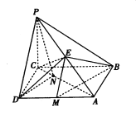
(1)求證:![]() 平面
平面![]() ;
;
(2)已知點(diǎn)![]() 是
是![]() 的中點(diǎn),點(diǎn)
的中點(diǎn),點(diǎn)![]() 是
是![]() 上一點(diǎn),且平面
上一點(diǎn),且平面![]() 平面
平面![]() .若
.若![]() ,求點(diǎn)
,求點(diǎn)![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】三維柱形圖中柱的高度表示的是( )
A. 各分類變量的頻數(shù) B. 分類變量的百分比
C. 分類變量的樣本數(shù) D. 分類變量的具體值
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,四棱柱![]() 中,側(cè)棱
中,側(cè)棱![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為
為![]() 的中點(diǎn).
的中點(diǎn).

(1)證明:![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)設(shè)點(diǎn)![]() 在線段
在線段![]() 上,且直線
上,且直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】對于數(shù)25,規(guī)定第1次操作為23+53=133,第2次操作為13+33+33=55,如此反復(fù)操作,則第2 017次操作后得到的數(shù)是( )
A. 25 B. 250
C. 55 D. 133
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() ,當(dāng)點(diǎn)
,當(dāng)點(diǎn)![]() 在
在![]() 的圖象上運(yùn)動(dòng)時(shí),點(diǎn)
的圖象上運(yùn)動(dòng)時(shí),點(diǎn)![]() 在函數(shù)
在函數(shù)![]() 的圖象上運(yùn)動(dòng)(
的圖象上運(yùn)動(dòng)(![]() ).
).
(Ⅰ)求![]() 和
和![]() 的表達(dá)式;
的表達(dá)式;
(Ⅱ)已知關(guān)于![]() 的方程
的方程![]() 有實(shí)根,求實(shí)數(shù)
有實(shí)根,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(Ⅲ)設(shè)![]() ,函數(shù)
,函數(shù)![]() 的值域?yàn)?/span>
的值域?yàn)?/span>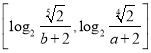 ,求實(shí)數(shù)
,求實(shí)數(shù)![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若4名學(xué)生報(bào)名參加數(shù)學(xué)、計(jì)算機(jī)、航模興趣小組,每人選報(bào)1項(xiàng),則不同的報(bào)名方式有__________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 是偶函數(shù).
是偶函數(shù).
(1)求![]() 的值;
的值;
(2)若函數(shù)![]() ,是否存在實(shí)數(shù)
,是否存在實(shí)數(shù)![]() 使得
使得![]() 最小值為0,若存在,求出
最小值為0,若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com