
【題目】如圖,在四棱錐![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 是矩形,
是矩形,![]() ,
,![]() 是
是![]() 的中點.
的中點.
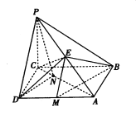
(1)求證:![]() 平面
平面![]() ;
;
(2)已知點![]() 是
是![]() 的中點,點
的中點,點![]() 是
是![]() 上一點,且平面
上一點,且平面![]() 平面
平面![]() .若
.若![]() ,求點
,求點![]() 到平面
到平面![]() 的距離.
的距離.
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,
(1)試證明函數![]() 是偶函數;
是偶函數;
(2)畫出![]() 的圖象;(要求先用鉛筆畫出草圖,再用黑色簽字筆描摹,否則不給分)
的圖象;(要求先用鉛筆畫出草圖,再用黑色簽字筆描摹,否則不給分)
(3)請根據圖象指出函數![]() 的單調遞增區間與單調遞減區間;(不必證明)
的單調遞增區間與單調遞減區間;(不必證明)
(4)當實數![]() 取不同的值時,討論關于
取不同的值時,討論關于![]() 的方程
的方程![]() 的實根的個數;(不必求出方程的解)
的實根的個數;(不必求出方程的解)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】△ABC的內角A,B,C所對應的邊分別為a,b,c.
(Ⅰ)若a,b,c成等差數列,證明:sinA+sinC=2sin(A+C);
(Ⅱ)若a,b,c成等比數列,求cosB的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=sin(π﹣ωx)cosωx+cos2ωx(ω>0)的最小正周期為π.
(Ⅰ)求ω的值;
(Ⅱ)將函數y=f(x)的圖象上各點的橫坐標縮短到原來的![]() ,縱坐標不變,得到函數y=g(x)的圖象,求函數y=g(x)在區間
,縱坐標不變,得到函數y=g(x)的圖象,求函數y=g(x)在區間![]() 上的最小值.
上的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了參加市高中籃球比賽,某中學決定從四個籃球較強的班級的籃球隊員中選出![]() 人組成男子籃球隊,代表該地區參賽,四個籃球較強的班級籃球隊員人數如下表:
人組成男子籃球隊,代表該地區參賽,四個籃球較強的班級籃球隊員人數如下表:
班級 | 高三(7)班 | 高三(17)班 | 高二(31)班 | 高二(32)班 |
人數 | 12 | 6 | 9 | 9 |
(1)現采取分層抽樣的方法從這四個班中抽取運動員,求應分別從這四個班抽出的隊員人數;
(2)該中學籃球隊奮力拼搏,獲得冠軍.若要從高三年級抽出的隊員中選出兩位隊員作為冠軍的代表發言,求選出的兩名隊員來自同一班的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】學校某研究性學習小組在對學生上課注意力集中情況的調查研究中,發現其在40分鐘的一節課中,注意力指數![]() 與聽課時間
與聽課時間![]() (單位:分鐘)之間的關系滿足如圖所示的圖象,當
(單位:分鐘)之間的關系滿足如圖所示的圖象,當![]() 時,圖象是二次函數圖象的一部分,其中頂點
時,圖象是二次函數圖象的一部分,其中頂點![]() ,過點
,過點![]() ;當
;當![]() 時,圖象是線段
時,圖象是線段![]() ,其中
,其中![]() .根據專家研究,當注意力指數大于62時,學習效果最佳.
.根據專家研究,當注意力指數大于62時,學習效果最佳.

(1)試求![]() 的函數關系式;
的函數關系式;
(2)教師在什么時段內安排內核心內容,能使得學生學習效果最佳?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正方體ABCD-A1B1C1D1的棱長為1,P為BC的中點,Q為線段CC1上的動點,過點A,P,Q的平面截該正方體所得的截面記為S,則下列命題正確的是 .(填序號)
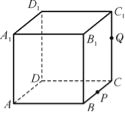
①當0<CQ<![]() 時,S為四邊形;
時,S為四邊形;
②當CQ=![]() 時,S為等腰梯形;
時,S為等腰梯形;
③當CQ=![]() 時,S與C1D1的交點R滿足C1R=
時,S與C1D1的交點R滿足C1R=![]() ;
;
④當![]() <CQ<1時,S為六邊形;
<CQ<1時,S為六邊形;
⑤當CQ=1時,S的面積為![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知圓
中,已知圓![]() 和圓
和圓![]() .
.

(1)若直線![]() 過點
過點![]() ,且被圓
,且被圓![]() 截得的弦長為
截得的弦長為![]() 是,求直線
是,求直線![]() 的方程;
的方程;
(2)設![]() 為平面上的點,滿足:存在過點
為平面上的點,滿足:存在過點![]() 的無窮多對互相垂直的直線
的無窮多對互相垂直的直線![]() 和
和![]() ,它們分別與圓
,它們分別與圓![]() 和圓
和圓![]() 相交,且直線
相交,且直線![]() 與被圓
與被圓![]() 截得的弦長與直線
截得的弦長與直線![]() 被圓
被圓![]() 截得的弦長相等,試求所有滿足條件的點
截得的弦長相等,試求所有滿足條件的點![]() 的坐標.
的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com