
【題目】已知橢圓![]() (
(![]() ),四點
),四點![]() ,
, ![]() ,
, 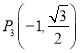 ,
, 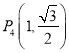 中恰有三點在橢圓上.
中恰有三點在橢圓上.
(1)求![]() 的方程;
的方程;
(2)設直線![]() 不經過
不經過![]() 點且與
點且與![]() 相交于
相交于![]() 兩點,若直線
兩點,若直線![]() 與直線
與直線![]() 的斜率之和為
的斜率之和為![]() ,證明:
,證明: ![]() 過定點.
過定點.
【答案】(1)![]() ;(2)見解析.
;(2)見解析.
【解析】試題分析:(1)根據橢圓的對稱性,得到![]() ,
, 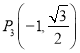 ,
, 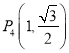 , 三點在橢圓C上.把點坐標代入橢圓C,求出a2=4,b2=1,由此能求出橢圓C的方程.
, 三點在橢圓C上.把點坐標代入橢圓C,求出a2=4,b2=1,由此能求出橢圓C的方程.
(2)設直線l: ![]() ,,不設直線P2A與直線P2B的斜率分別為k1,k2, 聯立直線P2A與橢圓方程得
,,不設直線P2A與直線P2B的斜率分別為k1,k2, 聯立直線P2A與橢圓方程得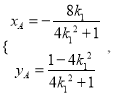 代入直線l方程:
代入直線l方程: ![]() 中得
中得![]() ,同理
,同理![]() ,所以易知k1,k2 ,是方程
,所以易知k1,k2 ,是方程![]() 兩根,由韋達定理
兩根,由韋達定理![]() ,即可得解.
,即可得解.
試題解析:
(1)由于p3,p4兩點關于y軸對稱,故由題設知C經過p3,p4兩點,又由![]() 知,C不經過點
知,C不經過點 ![]() ,所以點
,所以點![]() 在C上
在C上
因此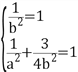 ,解得
,解得![]()
故C的方程為![]()
(2)由題設易知,直線l與x軸不平行,故可設方程為:![]() ,
,
設直線P2A與直線P2B的斜率分別為k1,k2 ,
聯立直線P2A與橢圓方程 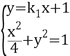
![]()
即![]() 代入
代入![]() 直線方程得
直線方程得![]() .
.
即 代入直線l方程:
代入直線l方程: ![]() 中,
中,
化簡得:![]()
同理: ![]()
易知k1,k2 ,是方程![]() 兩根
兩根
故k1+k2 =![]()
![]() m=t+2
m=t+2
即直線l為:![]()
![]()
即l過定點(2,-1).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,以
中,以![]() 為極點,
為極點, ![]() 軸正半軸為極軸建立極坐標系,直線
軸正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() (
(![]() ),
),![]() 為
為![]() 上一點,以
上一點,以![]() 為邊作等邊三角形
為邊作等邊三角形![]() ,且
,且![]() 、
、![]() 、
、![]() 三點按逆時針方向排列.
三點按逆時針方向排列.
(Ⅰ)當點![]() 在
在![]() 上運動時,求點
上運動時,求點![]() 運動軌跡的直角坐標方程;
運動軌跡的直角坐標方程;
(Ⅱ)若曲線![]() :
: ![]() ,經過伸縮變換
,經過伸縮變換![]() 得到曲線
得到曲線![]() ,試判斷點
,試判斷點![]() 的軌跡與曲線
的軌跡與曲線![]() 是否有交點,如果有,請求出交點的直角坐標,沒有則說明理由.
是否有交點,如果有,請求出交點的直角坐標,沒有則說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左,右焦點為
的左,右焦點為![]() ,左,右頂點為
,左,右頂點為![]() ,過點
,過點![]() 的
的
直線![]() 分別交橢圓于點
分別交橢圓于點![]() .
.
(1)設動點![]() ,滿足
,滿足![]() ,求點
,求點![]() 的軌跡方程;
的軌跡方程;
(2)當![]() 時,求
時,求![]() 點的坐標;
點的坐標;
(3)設![]() ,求證:直線
,求證:直線![]() 過
過![]() 軸上的定點.
軸上的定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖在四面體ABCD中,若截面PQMN是正方形,則在下列命題中正確的有 .(填上所有正確命題的序號)
①AC⊥BD
②AC=BD
③AC∥截面PQMN
④異面直線PM與BD所成的角為45°.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某手機賣場對市民進行國產手機認可度的調查,隨機抽取![]() 名市民,按年齡(單位:歲)進行統計和頻數分布表和頻率分布直線圖如下:
名市民,按年齡(單位:歲)進行統計和頻數分布表和頻率分布直線圖如下:
分組(歲) | 頻數 |
|
|
|
|
|
|
|
|
|
|
合計 |
|
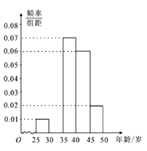
(1)求頻率分布表中![]() 、
、![]() 的值,并補全頻率分布直方圖;
的值,并補全頻率分布直方圖;
(2)在抽取的這![]() 名市民中,按年齡進行分層抽樣,抽取
名市民中,按年齡進行分層抽樣,抽取![]() 人參加國產手機用戶體驗問卷調查,現從這
人參加國產手機用戶體驗問卷調查,現從這![]() 人中隨機選取
人中隨機選取![]() 人各贈送精美禮品一份,設這
人各贈送精美禮品一份,設這![]() 名市民中年齡在
名市民中年齡在![]() 內的人數
內的人數![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
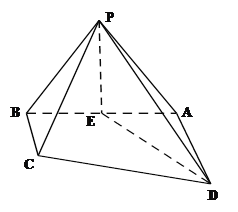
【題目】如圖,四棱錐P—ABCD中,底面ABCD是直角梯形,∠DAB=90°,AD//BC,且BC⊥PB,△PAB是等邊三角形,DA=AB=2,BC=![]() AD,E是線段AB的中點.
AD,E是線段AB的中點.
(I)求證:PE⊥CD;
(II)求PC與平面PDE所成角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com