
(本題滿分13分)在△ABC中,角A、B、C所對的邊分別為a、b、c,向量 =
= ,
, =(cos2A,2sinA),且
=(cos2A,2sinA),且 ∥
∥ .
.
(1)求sinA的值;
(2)若b=2,△ABC的面積為3,求a.
(1)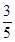 ;(2) 當cosA=
;(2) 當cosA=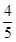 時, a=
時, a=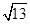 ;當cosA=-
;當cosA=-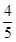 時, a=3
時, a=3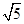 。
。
解析試題分析:(1)∵ ∥
∥ ,∴
,∴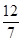 cos2A=(1-sinA)·2sinA, 3分
cos2A=(1-sinA)·2sinA, 3分
∴6(1-2sin2A)=7sinA(1-sinA)⇒5sin2A+7sinA-6=0,
∴sinA=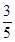 或sinA=-2(舍去). 6分
或sinA=-2(舍去). 6分
(2)由S△ABC= bcsinA=3,b=2,sinA=
bcsinA=3,b=2,sinA=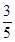 ,得c=5, 8分
,得c=5, 8分
又cosA=±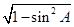 =±
=±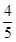 ,
,
∴a2=b2+c2-2bccosA=4+25-2×2×5cosA=29-20cosA, 10分
當cosA=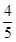 時,a2=13⇒a=
時,a2=13⇒a=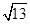 ;
;
當cosA=-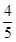 時,a2=45⇒a=3
時,a2=45⇒a=3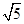 . 13分
. 13分
考點:數量積;向量共線的條件;余弦定理;三角形的面積公式。
點評:本題是一個三角函數同向量結合的問題,是以向量平行條件,得到三角函數的關系式,是一道綜合題,在高考時可以選擇和填空形式出現,也可以作為解答題的一部分出現。


 寒假大串聯黃山書社系列答案
寒假大串聯黃山書社系列答案 寒假創新型自主學習第三學期寒假銜接系列答案
寒假創新型自主學習第三學期寒假銜接系列答案科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
已知函數f(x)=" cos(" 2x+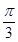 )+sin2x.
)+sin2x.
(Ⅰ)求函數f(x)的最小正周期和值域;
(Ⅱ)在△ABC中,角A、B、C的對邊分別為a、b、c,滿足
2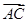 ·
·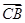 =
=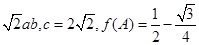 , 求△ABC的面積S.
, 求△ABC的面積S.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com