
如圖:四棱錐P―ABCD底面為一直角梯形,
![]()
![]() ,E是PC中點.
,E是PC中點.
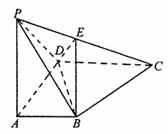
(1)求證:平面![]()
(2)求證:![]()
(3)假定![]() 的平面角的正切值
的平面角的正切值
解法一:(1)∵PA⊥平面ABCD, ∴PA⊥DC,
∵DC⊥AD且AD∩PA=A, ∴DC⊥面PAD。
∴DC![]() 面PDC。 ∴平面PDC⊥平面PAD。
面PDC。 ∴平面PDC⊥平面PAD。
(2)證明:取PD中點F,連接EF,FA。
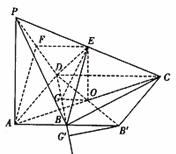
∵E為PC中點,
∴在△PDC中,EF![]() , ∴EF
, ∴EF![]() AB。
AB。
∴ 四邊形ABEF為平行四邊形,即BE//AF。
∵ AF![]() 面PAD且BE
面PAD且BE![]() 面PAD, ∴BE//平面PAD。
面PAD, ∴BE//平面PAD。
(3)解:連接AC,取AC中點O,連接EO。
在△APC中,EO![]() PA。
PA。
∵PA⊥平面ABCD, ∴EO⊥平面ABCD。
過O作OG⊥BD交BD于G,連接EG。
由三垂線定理知:∠EGO為所求二面角E―BD―C的平面角。
設PA=AD=CD=2a,AB=a,∴EO=a
連DO并延長交AB于B′,則四邊形AB ′CD為正方形,且B′B=a
O為DB′中點,過B′作B′G′⊥DB于G′
∴OG=![]()
![]()
在△EOG中,tan∠EGO=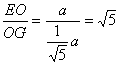 ,
,
故二面角E―BD―C的平面角的正切值為![]()
解法二:(1)同解法一
(2)同解法一
(3)如圖建立空間直角坐標系,設AB=a,
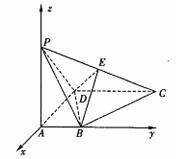
則B(0,a,0),D(-2 a,0,0),C(-2a,2 a,0)
P(0,0,2a),A(0,0,0)
∴![]()
∴![]()
∵PA⊥平面ABCD,
∴![]() 是平面ABCD的一個法向量,且
是平面ABCD的一個法向量,且![]()
設平面BDE的一個法向量為m=(x,y,z)
則m⊥![]()
∴m?![]()
得![]()
令z=1 則m=(1,-2,1)
設![]() 與m所成角為
與m所成角為![]()
則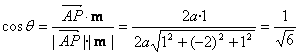
∴![]()
∴二面角E―BD―C的平面角的正切值為![]()


 仁愛英語同步練習冊系列答案
仁愛英語同步練習冊系列答案 學習實踐園地系列答案
學習實踐園地系列答案科目:高中數學 來源: 題型:
 如圖,四棱錐P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
如圖,四棱錐P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,四棱錐P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,側面PAD⊥底面ABCD,且△PAD為等腰直角三角形,∠APD=90°,M為AP的中點.
如圖,四棱錐P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,側面PAD⊥底面ABCD,且△PAD為等腰直角三角形,∠APD=90°,M為AP的中點.查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,四棱錐P-ABCD的底面ABCD是矩形,AB=2,BC=
如圖,四棱錐P-ABCD的底面ABCD是矩形,AB=2,BC=| 2 |
| AE |
| AP |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,四棱錐P-ABCD中,底面ABCD為矩形,PA⊥底面ABCD,且PA=AB=1,AD=
如圖,四棱錐P-ABCD中,底面ABCD為矩形,PA⊥底面ABCD,且PA=AB=1,AD=| 3 |
| ||
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,四棱錐P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=2
如圖,四棱錐P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=2| 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com