
分析 (1)求函數定義域、導數,按照a≥0,a<0兩種情況討論f′(x)的符號變化,由極值定義可得結論;
(2)先由條件求出g(x),存在x∈(0,+∞),使得g(x)<$\frac{x-m+3}{\sqrt{x}}$成立,即m<x-$\sqrt{x}$ex+3成立.令h(x)=x-$\sqrt{x}$ex+3,x∈(0,+∞),則問題等價于m<h(x)max,利用導數基本不等式可求得h(x)max;
(3)當a=0時,令φ(x)=g(x)-f(x)-2=ex-lnx-2,利用導數表示出φ(x)的最小值,只需說明最小值大于零即可.
解答 解:(1)∵f(x)=ax+lnx,x>0,
∴f′(x)=a+$\frac{1}{x}$,
當a≥0時,f′(x)>0恒成立,
∴f(x)在(0,+∞)上單調遞增,函數無極值,
當a<0時,
令f′(x)>0,解得0<x<-$\frac{1}{a}$,函數f(x)單調遞增,
令f′(x)<0,解得x>-$\frac{1}{a}$,函數f(x)單調遞減,
當x=-$\frac{1}{a}$時,函數有極大值,極大值為f(-$\frac{1}{a}$)=-1+ln(-$\frac{1}{a}$)=-1-ln(-a),無極小值;
(2)證明:?x∈(0,+∞),使得g(x)<$\frac{x-m+3}{\sqrt{x}}$成立.
∴?x∈(0,+∞),m<x+3-$\sqrt{x}$ex,
設h(x)=x+3-$\sqrt{x}$ex,
∴m<h(x)max,
∴h′(x)=1-ex($\frac{1}{2}{x}^{-\frac{1}{2}}$+${x}^{\frac{1}{2}}$),
∵$\frac{1}{2}{x}^{-\frac{1}{2}}$+${x}^{\frac{1}{2}}$≥2$\sqrt{\frac{1}{2}{x}^{-\frac{1}{2}}•{x}^{\frac{1}{2}}}$=$\sqrt{2}$,
∴h′(x)<0,
∴h(x)在(0,+∞)上為減函數,
∴h(x)<h(0)=3,
∴m≤3,
故m的取值范圍為(-∞,3];
(3)a=0時,f(x)=lnx
令φ(x)=g(x)-f(x)-2,則φ(x)=ex-lnx-2,
∴φ′(x)=ex-$\frac{1}{x}$,且φ'(x)在(0,+∞)上為增函數,
設φ′(x)=0的根為x=t,則et=$\frac{1}{t}$,即t=e-t,
∵當x∈(0,t)時,φ'(x)<0,φ(x)在(0,t)上為減函數,
當x∈(t,+∞)時,φ'(x)>0,φ(x)在(t,+∞)上為增函數,
∴φ(x)min=φ(t)=et-lnt-2=et-lne-t-2=et+t-2.
∵φ'(1)=e-1>0,φ′($\frac{1}{2}$)=$\sqrt{e}$-2,
∴t∈($\frac{1}{2}$,1)
由于函數y=ex+x-2在上為增函數,
∴φ(x)min=φ(t)=et+t-2>e,
∴g(x)-f(x)>2.
點評 該題考查恒成立問題、利用導數研究函數的極值最值,考查基本不等式,考查分類整合思想、轉化思想,考查學生綜合運用知識分析解決問題的能力.注意認真體會(3)問中二次求導的應用.


科目:高中數學 來源:2017屆安徽合肥一中高三上學期月考一數學(文)試卷(解析版) 題型:選擇題
下列說法中正確的是( )
A.“ ”是“函數
”是“函數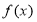 是奇函數”的充要條件
是奇函數”的充要條件
B.命題“若 ,則
,則 ”的否命題是“若
”的否命題是“若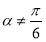 ,則
,則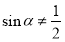 ”
”
C.若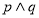 為假命題,則
為假命題,則 均為假命題
均為假命題
D.若 ,
, ,則
,則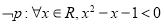
查看答案和解析>>
科目:高中數學 來源:2016-2017學年河北正定中學高二上月考一數學(文)試卷(解析版) 題型:選擇題
觀察下列散點圖,其中兩個變量的相關關系判斷正確的是( )
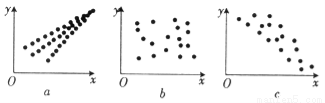
A. 為正相關,
為正相關,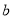 為負相關,
為負相關,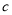 為不相關
為不相關
B.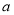 為負相關,
為負相關,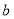 為不相關,
為不相關,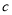 為正相關
為正相關
C.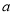 為負相關,
為負相關,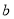 為正相關,
為正相關,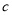 為不相關
為不相關
D.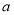 為正相關,
為正相關,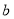 為不相關,
為不相關, 為負相關
為負相關
查看答案和解析>>
科目:高中數學 來源:2016-2017學年河北正定中學高二上月考一數學(理)試卷(解析版) 題型:選擇題
運行下面的程序,若 ,則輸出的
,則輸出的 等于( )
等于( )

A.9 B.7 C.13 D.11
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
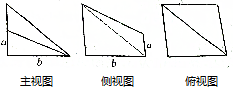
| A. | 4$\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $2\sqrt{2}$ | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,在五棱錐P-ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC,∠ABC=45°,AB=2$\sqrt{2}$,BC=2AE=4,三角形PAB是等腰三角形.
如圖,在五棱錐P-ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC,∠ABC=45°,AB=2$\sqrt{2}$,BC=2AE=4,三角形PAB是等腰三角形.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com