
分析 (Ⅰ)將C參數方程化為普通方程,利用$\left\{\begin{array}{l}x=ρcosθ\\ y=ρsinθ\end{array}\right.$代入,可得曲線C 的極坐標方程.
(Ⅱ)法一:利用參數的幾何意義,求|OB|,|OA|,∠AOB=60°,即可求△AOB的面積,
法二:在平面直角坐標系中,根據l1:θ=$\frac{π}{6}$,l2:θ=$\frac{π}{3}$,求出方程與圓C求解交點A和B,|OB|,|OA|,∠AOB=60°,即可求△AOB的面積,
解答 解:(Ⅰ)∵曲線C的參數方程為$\left\{\begin{array}{l}x=2+\sqrt{5}cosα\\ y=1+\sqrt{5}sinα\end{array}\right.$(α為參數),利用sin2α+cos2α=1,
$\sqrt{5}sinα=x-2$,$\sqrt{5}cosα$=y-1,可得:(x-2)2+(y-1)2=5.
∴曲線C的普通方程為(x-2)2+(y-1)2=5.
將$\left\{\begin{array}{l}x=ρcosθ\\ y=ρsinθ\end{array}\right.$代入并化簡得:ρ=4cosθ+2sinθ
即曲線C的極坐標方程為ρ=4cosθ+2sinθ.
(Ⅱ)解法一:在極坐標系中,C:ρ=4cosθ+2sinθ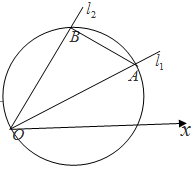
∴由$\left\{{\begin{array}{l}{θ=\frac{π}{6}}\\{ρ=4cosθ+2sinθ}\end{array}}\right.$得到$|{OA}|=2\sqrt{3}+1$;
同理$|{OB}|=2+\sqrt{3}$.
又∵$∠AOB=\frac{π}{6}$
∴${S_{△AOB}}=\frac{1}{2}|{OA}|•|{OB}|sin∠AOB=\frac{{8+5\sqrt{3}}}{4}$.
即△AOB的面積為$\frac{{8+5\sqrt{3}}}{4}$.…(10分)
解法二:在平面直角坐標系中,C:(x-2)2+(y-1)2=5
l1:θ=$\frac{π}{6}$,l2:θ=$\frac{π}{3}$,可得${l_1}:y=\frac{{\sqrt{3}}}{3}x$,${l_2}:y=\sqrt{3}x$
∴由$\left\{{\begin{array}{l}{y=\frac{{\sqrt{3}}}{3}x}\\{{{({x-2})}^2}+{{({y-1})}^2}=5}\end{array}}\right.$得$A({\frac{{6+\sqrt{3}}}{2},\frac{{2\sqrt{3}+1}}{2}})$
∴$|{OA}|=2\sqrt{3}+1$
同理$B({\frac{{2+\sqrt{3}}}{2},\frac{{2\sqrt{3}+3}}{2}})$
∴$|{OA}|=2\sqrt{3}+1$,$|{OB}|=2+\sqrt{3}$
又∵$∠AOB=\frac{π}{6}$
∴${S_{△AOB}}=\frac{1}{2}|{OA}|•|{OB}|sin∠AOB=\frac{{8+5\sqrt{3}}}{4}$
即△AOB的面積為$\frac{{8+5\sqrt{3}}}{4}$.
點評 本題主要考查了參數方程,極坐標方程與普通方程的換算.參數方程的幾何意義的運用.屬于中檔題.


科目:高中數學 來源: 題型:解答題
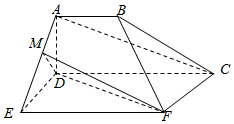 如圖,空間幾何體ADE-BCF中,四邊形ABCD是梯形,四邊形CDEF
如圖,空間幾何體ADE-BCF中,四邊形ABCD是梯形,四邊形CDEF查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 是否愿意提供志愿者服務 性別 | 愿意 | 不愿意 |
| 男生 | 25 | 5 |
| 女生 | 15 | 15 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 向右平移$\frac{π}{4}$個單位長度 | B. | 向右平移$\frac{π}{12}$個單位長度 | ||
| C. | 向左平移$\frac{π}{4}$個單位長度 | D. | 向左平移$\frac{π}{12}$個單位長度 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
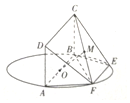 如圖,AB為圓O的直徑,點E,F在圓O上,AB∥EF,矩形ABCD所在的平面和圓(x-1)2+y2=1所在的平面互相垂直,且AB=2,AD=EF=1,∠BAF=60°.
如圖,AB為圓O的直徑,點E,F在圓O上,AB∥EF,矩形ABCD所在的平面和圓(x-1)2+y2=1所在的平面互相垂直,且AB=2,AD=EF=1,∠BAF=60°.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com