Question

20．變量x，y滿足約束條件$\left\{\begin{array}{l}x+y≥0\\ x-2y+2≥0\\ mx-y≤0\end{array}\right.$若2x-y的最大值是2，則約束條件表示的平面區域面積為（　　）

• A． $\frac{8}{15}$
• B． $\frac{8}{3}$
• C． $\frac{4}{3}$
• D． $\frac{2}{3}$

Answer 1

分析 由約束條件作出可行域，化目標函數為直線方程的斜截式，數形結合得到最優解，聯立方程組求得最優解的坐標，代入目標函數求得m的值

解答 解：由約束條件$\left\{\begin{array}{l}x+y≥0\\ x-2y+2≥0\\ mx-y≤0\end{array}\right.$作出可行域如圖，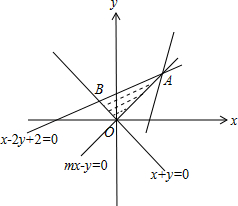
聯立$\left\{\begin{array}{l}{x-2y+2=0}\\{mx-y=0}\end{array}\right.$，解得A（$\frac{2}{2m-1}$，$\frac{2m}{2m-1}$），
化目標函數z=2x-y為y=2x-z，
由圖可知，當直線過A時，直線在y軸上的截距最小，
z有最大值為$\frac{4}{2m-1}$-$\frac{2m}{2m-1}$=2，
解得：m=1．
A（2，2），B（$-\frac{2}{3}$，$\frac{2}{3}$），
由OA⊥OB，得到平面區域面積為$\frac{1}{2}×2\sqrt{2}×\frac{2}{3}\sqrt{2}$=$\frac{4}{3}$；
故選C．

點評 本題考查了簡單的線性規劃，考查了數形結合的解題思想方法，是中檔題．