
已知函數(shù)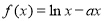 ,
,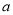 為常數(shù).
為常數(shù).
(1)若函數(shù)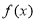 在
在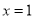 處的切線與
處的切線與 軸平行,求
軸平行,求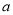 的值;
的值;
(2)當(dāng)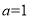 時(shí),試比較
時(shí),試比較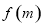 與
與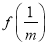 的大小;
的大小;
(3)若函數(shù)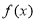 有兩個(gè)零點(diǎn)
有兩個(gè)零點(diǎn)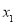 、
、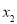 ,試證明
,試證明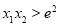 .
.
(1)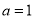 ;(2)①當(dāng)
;(2)①當(dāng)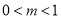 時(shí),
時(shí),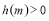 ,即
,即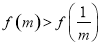 ;②當(dāng)
;②當(dāng)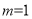 時(shí),
時(shí),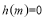
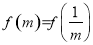 ;③當(dāng)
;③當(dāng)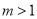 時(shí),
時(shí),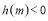 即
即 ;(3)詳見解析
;(3)詳見解析
【解析】
試題分析:(1)根據(jù)題意切線平行于x軸即斜率為0,則對函數(shù)求導(dǎo)可得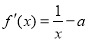 ,即
,即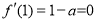 ,可求出a;(2)根據(jù)題意當(dāng)
,可求出a;(2)根據(jù)題意當(dāng)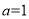 時(shí),函數(shù)就確定下來了
時(shí),函數(shù)就確定下來了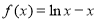 ,對其求導(dǎo)可得
,對其求導(dǎo)可得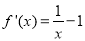 ,可研究出函數(shù)的單調(diào)性情況,為了比較大小可引入一個(gè)新的函數(shù),即令
,可研究出函數(shù)的單調(diào)性情況,為了比較大小可引入一個(gè)新的函數(shù),即令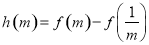 ,則利用導(dǎo)數(shù)對其進(jìn)行研究可得
,則利用導(dǎo)數(shù)對其進(jìn)行研究可得 ,而
,而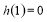 ,則可由m與1的大小關(guān)系進(jìn)行分類得出結(jié)論;(3)顯然兩零點(diǎn)均為正數(shù),故不妨設(shè)
,則可由m與1的大小關(guān)系進(jìn)行分類得出結(jié)論;(3)顯然兩零點(diǎn)均為正數(shù),故不妨設(shè)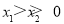 ,由零點(diǎn)的定義可得:
,由零點(diǎn)的定義可得: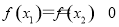 ,即
,即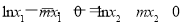 ,觀察此兩式的結(jié)構(gòu)特征可相加也可相減化簡得:
,觀察此兩式的結(jié)構(gòu)特征可相加也可相減化簡得: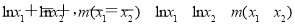 ,現(xiàn)在我們要證明
,現(xiàn)在我們要證明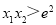 ,即證明
,即證明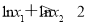 ,也就是
,也就是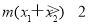 .又因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/GZSX/web/STSource/2014111719103755388648/SYS201411171910483824125780_DA/SYS201411171910483824125780_DA.026.png">,所以即證明
.又因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/GZSX/web/STSource/2014111719103755388648/SYS201411171910483824125780_DA/SYS201411171910483824125780_DA.026.png">,所以即證明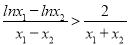 ,即
,即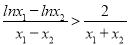 .由它的結(jié)構(gòu)可令
.由它的結(jié)構(gòu)可令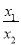 =t,則
=t,則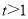 ,于是
,于是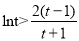 .構(gòu)造一新函數(shù)
.構(gòu)造一新函數(shù)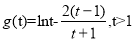 ,將問題轉(zhuǎn)化為求此函數(shù)的最小值大于零,即可得證.
,將問題轉(zhuǎn)化為求此函數(shù)的最小值大于零,即可得證.
(1)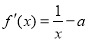 ,由題
,由題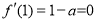 ,
,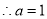 . 4分
. 4分
(2)當(dāng)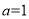 時(shí),
時(shí),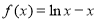 ,
,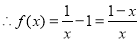 ,當(dāng)
,當(dāng)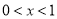 時(shí),
時(shí),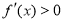 ,
,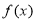 單調(diào)遞增,當(dāng)
單調(diào)遞增,當(dāng) 時(shí),
時(shí),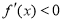 ,
,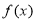 單調(diào)遞減.
單調(diào)遞減.
由題,令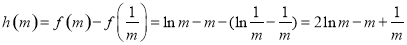 ,
,
則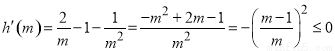 . 7分
. 7分
又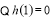 ,
,
①當(dāng)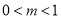 時(shí),
時(shí),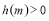 ,即
,即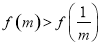 ;
;
②當(dāng)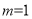 時(shí),
時(shí),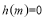
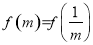 ;
;
③當(dāng)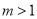 時(shí),
時(shí),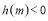 即
即 . 10分
. 10分
(3)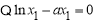 ,
,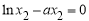 ,
,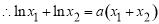 ,
,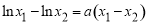 ,
,
 , 12分
, 12分
欲證明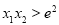 ,即證
,即證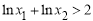 ,
,
因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/GZSX/web/STSource/2014111719103755388648/SYS201411171910483824125780_DA/SYS201411171910483824125780_DA.049.png">,
所以即證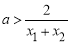 ,所以原命題等價(jià)于證明
,所以原命題等價(jià)于證明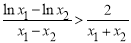 ,即證:
,即證: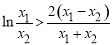
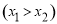 ,
,
令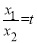 ,則
,則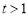 ,設(shè)
,設(shè)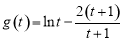
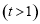 ,
,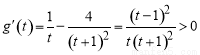 ,
,
所以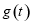 在
在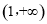 單調(diào)遞增,又因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/GZSX/web/STSource/2014111719103755388648/SYS201411171910483824125780_DA/SYS201411171910483824125780_DA.061.png">,所以
單調(diào)遞增,又因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/GZSX/web/STSource/2014111719103755388648/SYS201411171910483824125780_DA/SYS201411171910483824125780_DA.061.png">,所以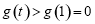 ,
,
所以 ,所以
,所以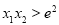 16分
16分
考點(diǎn):1.曲線的切線;2.函數(shù)與導(dǎo)數(shù)的運(yùn)用;3.不等式的證明



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源:2013-2014學(xué)年江蘇省連云港市高三3月第二次調(diào)研考試文科數(shù)學(xué)試卷(解析版) 題型:填空題
已知雙曲線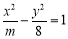 的離心率為
的離心率為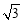 ,則實(shí)數(shù)m的值為 .
,則實(shí)數(shù)m的值為 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2013-2014學(xué)年江蘇省蘇、錫、常、鎮(zhèn)四市高三教學(xué)情況調(diào)查(一)理科數(shù)學(xué)試卷(解析版) 題型:填空題
若復(fù)數(shù)z =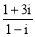 (
(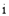 為虛數(shù)單位),則|z|= .
為虛數(shù)單位),則|z|= .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2013-2014學(xué)年江蘇省蘇、錫、常、鎮(zhèn)四市高三教學(xué)情況調(diào)查(一)文科數(shù)學(xué)試卷(解析版) 題型:填空題
執(zhí)行如圖所示的算法流程圖,則最后輸出的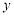 等于 .
等于 .
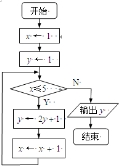
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2013-2014學(xué)年江蘇省鹽城市高三第三次模擬考試數(shù)學(xué)試卷(解析版) 題型:解答題
設(shè)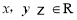 ,且滿足:
,且滿足: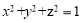 ,
, ,求證:
,求證: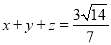 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2013-2014學(xué)年江蘇省鹽城市高三第三次模擬考試數(shù)學(xué)試卷(解析版) 題型:填空題
若實(shí)數(shù)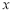 ,
,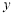 滿足
滿足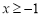 ,
,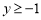 且
且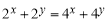 ,則
,則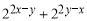 的取值范圍是 .
的取值范圍是 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2013-2014學(xué)年江蘇省淮安市高三5月信息卷理科數(shù)學(xué)試卷(解析版) 題型:解答題
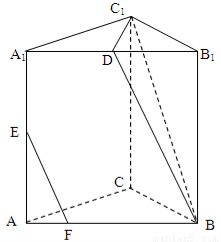
在正三棱柱ABC-A1B1C1中,AB=AA1,D、E分別是棱A1B1、AA1的中點(diǎn),點(diǎn)F在棱AB上,且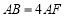 .
.
(1)求證:EF∥平面BDC1;
(2)求證: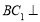 平面
平面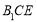 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2013-2014學(xué)年江蘇省淮安市高三Ⅲ級(jí)部決戰(zhàn)四統(tǒng)測二理科數(shù)學(xué)試卷(解析版) 題型:解答題
在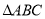 中,角
中,角 所對的邊分別為
所對的邊分別為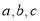 。已知
。已知 ,
,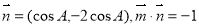 .
.
(1)若 ,求
,求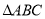 的面積; (2)求
的面積; (2)求 的值.
的值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com