
【題目】如圖,四邊形ABCD、ADEF為正方形,G,H是DF,FC的中點. 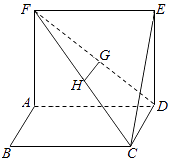
(1)求證:GH∥平面CDE;
(2)求證:BC⊥平面CDE.
【答案】
(1)證明:∵G,H是DF,FC的中點.
∴GH∥CD,
又GH平面CDE,CD平面CDE,
∴GH∥平面CDE
(2)證明:∵四邊形ABCD、ADEF為正方形,
∴DE⊥AD,CD⊥AD,BC∥AD.
又DE平面CDE,CD平面CDE,CD∩DE=D,
∴AD⊥平面CDE,
又BC∥AD,
∴BC⊥平面CDE
【解析】(1)由中位線定理得出GH∥CD,故GH∥平面CDE;(2)由AD⊥CD,AD⊥DE得出AD⊥平面CDE,而BC∥AD,故BC⊥平面CDE.
【考點精析】本題主要考查了直線與平面平行的判定和直線與平面垂直的判定的相關知識點,需要掌握平面外一條直線與此平面內的一條直線平行,則該直線與此平面平行;簡記為:線線平行,則線面平行;一條直線與一個平面內的兩條相交直線都垂直,則該直線與此平面垂直;注意點:a)定理中的“兩條相交直線”這一條件不可忽視;b)定理體現了“直線與平面垂直”與“直線與直線垂直”互相轉化的數學思想才能正確解答此題.


 教材全解字詞句篇系列答案
教材全解字詞句篇系列答案科目:高中數學 來源: 題型:
【題目】已知直線![]() 與拋物線
與拋物線![]() 相切,且與
相切,且與![]() 軸的交點為
軸的交點為![]() ,點
,點![]() .若動點
.若動點![]() 與兩定點
與兩定點![]() 所構成三角形的周長為6.
所構成三角形的周長為6.
(Ⅰ) 求動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ) 設斜率為![]() 的直線
的直線![]() 交曲線
交曲線![]() 于
于![]() 兩點,當
兩點,當![]() ,且
,且![]() 位于直線
位于直線![]() 的兩側時,證明:
的兩側時,證明: ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 中,
中, ![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,點
,點![]() 在
在![]() 上,且
上,且![]() .
.
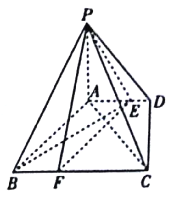
(Ⅰ)已知點![]() 在
在![]() 上,且
上,且![]() ,求證:平面
,求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)當二面角![]() 的余弦值為多少時,直線
的余弦值為多少時,直線![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ?
?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】教育學家分析發現加強語文樂隊理解訓練與提高數學應用題得分率有關,某校興趣小組為了驗證這個結論,從該校選擇甲乙兩個同軌班級進行試驗,其中甲班加強閱讀理解訓練,乙班常規教學無額外訓練,一段時間后進行數學應用題測試,統計數據情況如下面的![]() 列聯表(單位:人)
列聯表(單位:人)

(1)能夠據此判斷有97.5%把握熱內加強語文閱讀訓練與提高數學應用題得分率有關?
(2)經過多次測試后,小明正確解答一道數學應用題所用的時間在5—7分鐘,小剛正確解得一道數學應用題所用的時間在6—8分鐘,現小明、小剛同時獨立解答同一道數學應用題,求小剛比小明現正確解答完的概率;

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列{an}中,a1=1,an+an+1=( ![]() )n , Sn=a1+4a2+42a3+…+4n﹣1an , 類比課本中推導等比數列前項和公式的方法,可求得5Sn﹣4nan= .
)n , Sn=a1+4a2+42a3+…+4n﹣1an , 類比課本中推導等比數列前項和公式的方法,可求得5Sn﹣4nan= .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓![]() 經過不同的三點
經過不同的三點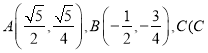 在第三象限),線段
在第三象限),線段![]() 的中點在直線
的中點在直線![]() 上.
上.
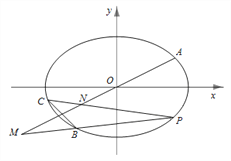
(Ⅰ)求橢圓![]() 的方程及點
的方程及點![]() 的坐標;
的坐標;
(Ⅱ)設點![]() 是橢圓
是橢圓![]() 上的動點(異于點
上的動點(異于點![]() 且直線
且直線![]() 分別交直線
分別交直線![]() 于
于![]() 兩點,問
兩點,問![]() 是否為定值?若是,求出定值;若不是,請說明理由.
是否為定值?若是,求出定值;若不是,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com