
【題目】函數f(x)=6cos2![]() sinωx﹣3(ω>0)在一個周期內的圖象如圖所示,A為圖象的最高點,B,C為圖象與x軸的交點,且△ABC為正三角形
sinωx﹣3(ω>0)在一個周期內的圖象如圖所示,A為圖象的最高點,B,C為圖象與x軸的交點,且△ABC為正三角形
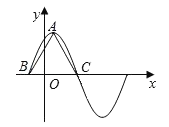
(1)求ω的值及函數f(x)的表達式;
(2)若f(x0)![]() ,且x0∈(
,且x0∈(![]() ),求f(x0+1)的值
),求f(x0+1)的值
【答案】(1)ω![]() ,f(x)=2
,f(x)=2![]() (2)
(2)![]()
【解析】
(1)利用兩角和公式和二倍角公式對函數解析式化簡,根據題意求得BC的長,進而求得三角函數的最小正周期,則ω可得.求得f(x)的表達式,根據三角函數的性質求得函數f(x)的值域.
(2)由![]() ,知
,知 ![]() x0
x0![]() ∈(
∈(![]() ,
,![]() ),由f(
),由f(![]() )
)![]() ,可求得即sin(
,可求得即sin(![]() )
)![]() ,利用兩角和的正弦公式即可求得f(
,利用兩角和的正弦公式即可求得f(![]() +1).
+1).
(1)函數f(x)=6cos2![]() sinωx﹣3=3cosωx
sinωx﹣3=3cosωx![]() sinωx=2
sinωx=2![]() sin(ωx
sin(ωx![]() ),由于△ABC為正三角形,所以三角形的高為
),由于△ABC為正三角形,所以三角形的高為![]() ,所以BC=4.
,所以BC=4.
所以函數f(x)的最小正周期為T=4×2=8,所以ω![]() ,
,
故得到f(x)=2![]() .
.
(2)由于若f(x0)![]() ,所以
,所以![]() ,整理得
,整理得![]() ,由于x0∈(
,由于x0∈(![]() )所以
)所以![]() ,所以
,所以![]() ,
,
所以f(x0+1)=2![]()
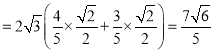


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,已知![]() 為坐標原點,點
為坐標原點,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的坐標為
的坐標為![]() ,其中
,其中![]() 且
且![]() .設
.設![]() .
.
(1)若![]() ,
,![]() ,
,![]() ,求方程
,求方程![]() 在區間
在區間![]() 內的解集;
內的解集;
(2)若點![]() 是直線
是直線![]() 上的動點.當
上的動點.當![]() 時,設函數
時,設函數![]() 的值域為集合
的值域為集合![]() ,不等式
,不等式![]() 的解集為集合
的解集為集合![]() .若
.若![]() 恒成立,求實數
恒成立,求實數![]() 的最大值;
的最大值;
(3)若函數![]() 滿足“圖像關于點
滿足“圖像關于點![]() 對稱,且在
對稱,且在![]() 處
處![]() 取得最小值”,求
取得最小值”,求![]() 、
、![]() 和
和![]() 滿足的充要條件.
滿足的充要條件.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】司機在開機動車時使用手機是違法行為,會存在嚴重的安全隱患,危及自己和他人的生命. 為了研究司機開車時使用手機的情況,交警部門調查了![]() 名機動車司機,得到以下統計:在
名機動車司機,得到以下統計:在![]() 名男性司機中,開車時使用手機的有
名男性司機中,開車時使用手機的有![]() 人,開車時不使用手機的有
人,開車時不使用手機的有![]() 人;在
人;在![]() 名女性司機中,開車時使用手機的有
名女性司機中,開車時使用手機的有![]() 人,開車時不使用手機的有
人,開車時不使用手機的有![]() 人.
人.
(1)完成下面的![]() 列聯表,并判斷是否有
列聯表,并判斷是否有![]() 的把握認為開車時使用手機與司機的性別有關;
的把握認為開車時使用手機與司機的性別有關;
開車時使用手機 | 開車時不使用手機 | 合計 | |
男性司機人數 | |||
女性司機人數 | |||
合計 |
(2)以上述的樣本數據來估計總體,現交警部門從道路上行駛的大量機動車中隨機抽檢3輛,記這3輛車中司機為男性且開車時使用手機的車輛數為![]() ,若每次抽檢的結果都相互獨立,求
,若每次抽檢的結果都相互獨立,求![]() 的分布列和數學期望
的分布列和數學期望![]() .
.
參考公式與數據:
參考數據:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
參考公式
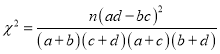 span>,其中
span>,其中![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某地區某種昆蟲產卵數和溫度有關.現收集了一只該品種昆蟲的產卵數![]() (個)和溫度
(個)和溫度![]() (
(![]() )的7組觀測數據,其散點圖如所示:
)的7組觀測數據,其散點圖如所示:
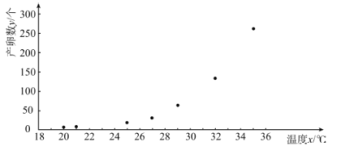
根據散點圖,結合函數知識,可以發現產卵數![]() 和溫度
和溫度![]() 可用方程
可用方程![]() 來擬合,令
來擬合,令![]() ,結合樣本數據可知
,結合樣本數據可知![]() 與溫度
與溫度![]() 可用線性回歸方程來擬合.根據收集到的數據,計算得到如下值:
可用線性回歸方程來擬合.根據收集到的數據,計算得到如下值:
|
|
|
|
|
|
27 | 74 |
| 182 |
|
|
表中![]() ,
,![]() .
.
(1)求![]() 和溫度
和溫度![]() 的回歸方程(回歸系數結果精確到
的回歸方程(回歸系數結果精確到![]() );
);
(2)求產卵數![]() 關于溫度
關于溫度![]() 的回歸方程;若該地區一段時間內的氣溫在
的回歸方程;若該地區一段時間內的氣溫在![]() 之間(包括
之間(包括![]() 與
與![]() ),估計該品種一只昆蟲的產卵數的范圍.(參考數據:
),估計該品種一只昆蟲的產卵數的范圍.(參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .)
.)
附:對于一組數據![]() ,
,![]() ,…,
,…,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為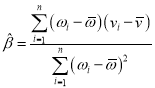 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為正方形,
為正方形,![]() 底面
底面![]() ,
,![]() ,
,![]() 為線段
為線段![]() 的中點.
的中點.
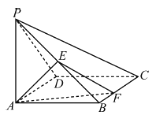
(1)若![]() 為線段
為線段![]() 上的動點,證明:平面
上的動點,證明:平面![]() 平面
平面![]() ;
;
(2)若![]() 為線段
為線段![]() ,
,![]() ,
,![]() 上的動點(不含
上的動點(不含![]() ,
,![]() ),
),![]() ,三棱錐
,三棱錐![]() 的體積是否存在最大值?如果存在,求出最大值;如果不存在,請說明理由.
的體積是否存在最大值?如果存在,求出最大值;如果不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】劉徽《九章算術商功》中將底面為長方形,兩個三角面與底面垂直的四棱錐體叫做陽馬.如圖,是一個陽馬的三視圖,則其外接球的體積為( )
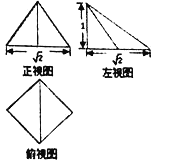
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】朱載堉(1536—1611),明太祖九世孫,音樂家、數學家、天文歷算家,在他多達百萬字的著述中以《樂律全書》最為著名,在西方人眼中他是大百科全書式的學者王子。他對文藝的最大貢獻是他創建了“十二平均律”,此理論被廣泛應用在世界各國的鍵盤樂器上,包括鋼琴,故朱載堉被譽為“鋼琴理論的鼻祖”。“十二平均律”是指一個八度有13個音,相鄰兩個音之間的頻率之比相等,且最后一個音頻率是最初那個音頻率的2倍,設第二個音的頻率為![]() ,第八個音的頻率為
,第八個音的頻率為![]() ,則
,則![]() 等于( )
等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,矩形![]() 中,
中,![]() 為
為![]() 的中點,將
的中點,將![]() 沿直線
沿直線![]() 翻折成
翻折成![]() ,連結
,連結![]() ,
,![]() 為
為![]() 的中點,則在翻折過程中,下列說法中所有正確的是( )
的中點,則在翻折過程中,下列說法中所有正確的是( )
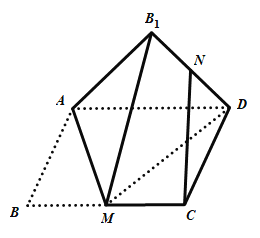
A.存在某個位置,使得![]()
B.翻折過程中,![]() 的長是定值
的長是定值
C.若![]() ,則
,則![]()
D.若![]() ,當三棱錐
,當三棱錐![]() 的體積最大時,三棱錐
的體積最大時,三棱錐![]() 的外接球的表面積是
的外接球的表面積是![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“移動支付、高鐵、網購、共享單車”被稱為中國的“新四大發明”.為了幫助50歲以上的中老年人更快地適應“移動支付”,某機構通過網絡組織50歲以上的中老年人學習移動支付相關知識.學習結束后,每人都進行限時答卷,得分都在![]() 內.在這些答卷(有大量答卷)中,隨機抽出
內.在這些答卷(有大量答卷)中,隨機抽出![]() 份,統計得分繪出頻率分布直方圖如圖.
份,統計得分繪出頻率分布直方圖如圖.
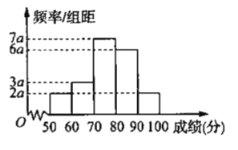
(1)求出圖中![]() 的值,并求樣本中,答卷成績在
的值,并求樣本中,答卷成績在![]() 上的人數;
上的人數;
(2)以樣本的頻率為概率,從參加這次答卷的人群中,隨機抽取![]() 名,記成績在
名,記成績在![]() 分以上(含
分以上(含![]() 分)的人數為
分)的人數為![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com