
(2)圓錐內有一半球,球面與圓錐側面相切,半球的底面在圓錐的底面上,已知半球半徑為r,圓錐的母線與底面所成的角為θ,求當圓錐的體積V圓錐=f(θ)最小時,圓錐的高h的值.
解析:(1)設母線與底面所成的角為θ,則底面半徑為cosθ,高h=sinθ.
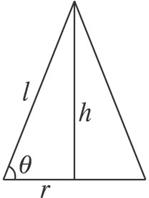
∴圓錐的體積V=![]() πcos2θsinθ=
πcos2θsinθ=![]() cos2θsinθ,
cos2θsinθ,
記μ=cos2θsinθ,
則μ2=cos4θsin2θ
=![]() [cos2θ·cos2θ·(2sin2θ)]
[cos2θ·cos2θ·(2sin2θ)]
≤![]() (
(![]() )3=
)3=![]() ,
,
∴μ≤![]() (當且僅當cos2θ=2sin2θ時,取“=”).
(當且僅當cos2θ=2sin2θ時,取“=”).
∴V≤![]() π,即V的最大值為
π,即V的最大值為![]() π,
π,
當V最大時,cos2θ=2sin2θ,
∴cosθ=![]() ,即圓錐的底面半徑為
,即圓錐的底面半徑為![]() .
.
另解:設底面半徑為r,高為h,則r2+h2=1,圓錐的體積為V=![]() πr2h,
πr2h,
∴V2=![]() r4h2=
r4h2=![]() (r2·r2·2h2)≤
(r2·r2·2h2)≤![]() .
.
(![]() )3=
)3=![]() ,即V≤
,即V≤![]() (當且僅當r2=2h2,即r=
(當且僅當r2=2h2,即r=![]() 時,取“=”).
時,取“=”).
(2)下圖是圓錐及其內切半球的軸截面,則圓錐的底面半徑為R=![]() ,圓錐的高h=
,圓錐的高h=![]() .
.
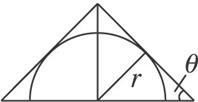
∴f(θ)=![]() πR2h=
πR2h=![]() πr3·
πr3·![]() .
.
由(1)的結論可知:當cosθ=![]() 時,sin2θcosθ取得最大值,從而f(θ)取得最小值,
時,sin2θcosθ取得最大值,從而f(θ)取得最小值,
即當h=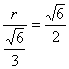 r時,f(θ)取得最小值.
r時,f(θ)取得最小值.


 口算題卡北京婦女兒童出版社系列答案
口算題卡北京婦女兒童出版社系列答案科目:高中數學 來源: 題型:
(2)圓錐內有一半球,球面與圓錐側面相切,半球的底面在圓錐的底面上,已知半球半徑為R,圓錐的母線與底面所成的角為θ,求當圓錐的體積V圓錐=f(θ)最小時,圓錐的高h的值.

圖1-1-4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com