
【題目】在四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .
.
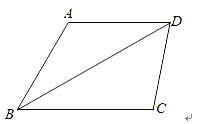
(1)求![]() 的長;
的長;
(2)若![]() ,求四邊形
,求四邊形![]() 的面積.
的面積.
【答案】(1)![]() (2)
(2) ![]()
【解析】
(1)由余弦定理得能求出AD的長.
(2)由正弦定理得![]() ,從而BC=3
,從而BC=3![]() ,DC
,DC![]() ,過A作AE⊥BD,交BD于E,過C作CF⊥BD,交BD于F,則可求AE
,過A作AE⊥BD,交BD于E,過C作CF⊥BD,交BD于F,則可求AE![]() ,CF
,CF![]() ,四邊形ABCD的面積:S=S△ABD+S△BDC
,四邊形ABCD的面積:S=S△ABD+S△BDC![]() ,由此能求出結果.
,由此能求出結果.
(1)∵在四邊形ABCD中,AD∥BC,AB![]() ,∠A=120°,BD=3.
,∠A=120°,BD=3.
∴由余弦定理得:cos120°![]() ,
,
解得AD![]() (舍去AD=﹣2
(舍去AD=﹣2![]() ),
),
∴AD的長為![]() .
.
(2)∵AD∥BC,AB![]() ,∠A=120°,BD=3,AD
,∠A=120°,BD=3,AD![]() ,
,
∠BCD=105°,
∴∠DBC=30°,∠BDC=45°,
∴![]() ,
,
解得BC=3![]() ,DC
,DC![]() ,
,
如圖,過A作AE⊥BD,交BD于E,過C作CF⊥BD,交BD于F,
則AE![]() ,CF
,CF![]() ,
,
∴四邊形ABCD的面積:
S=S△ABD+S△BDC![]()
![]()
![]() .
.


 狀元坊全程突破導練測系列答案
狀元坊全程突破導練測系列答案 直通貴州名校周測月考直通名校系列答案
直通貴州名校周測月考直通名校系列答案科目:高中數學 來源: 題型:
【題目】已知二次函數![]() .
.
(1)若![]() 的定義域和值域均是
的定義域和值域均是![]() ,求實數
,求實數![]() 的值;
的值;
(2)若![]() 在區間
在區間![]() 上是減函數,求
上是減函數,求![]() 在區間
在區間![]() 上的最小值和最大值;
上的最小值和最大值;
(3)若![]() 在區間
在區間![]() 上有零點,求實數
上有零點,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :在
:在![]() 軸上的一個焦點,與短軸兩個端點的連線互相垂直,且右焦點坐標為
軸上的一個焦點,與短軸兩個端點的連線互相垂直,且右焦點坐標為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設直線![]() 與圓
與圓![]() 相切,和橢圓交于
相切,和橢圓交于![]() ,
,![]() 兩點,
兩點,![]() 為原點,線段
為原點,線段![]() ,
,![]() 分別和圓
分別和圓![]() 交于
交于![]() ,
,![]() 兩點,設
兩點,設![]() ,
,![]() 的面積分別為
的面積分別為![]() ,
,![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合S={1,2,3,4,5,6},一一映射f:S→S滿足條件:對于任意的x∈S,有f(f(f(x)))=x。則滿足條件的映射f的個數是( )。
A. 81 B. 80 C. 40 D. 27
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com