解關于x的不等式ax2-2≥2x-ax(a∈R).
【答案】
分析:對a分類:a=0,a>0,-2<a<0,a=-2,a<-2,分別解不等式,求解取交集即可.
解答:解:原不等式變形為ax
2+(a-2)x-2≥0.
①a=0時,x≤-1;
②a≠0時,不等式即為(ax-2)(x+1)≥0,
當a>0時,x≥

或x≤-1;
由于
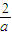
-(-1)=

,于是
當-2<a<0時,

≤x≤-1;
當a=-2時,x=-1;
當a<-2時,-1≤x≤

.
綜上,當a=0時,x≤-1;當a>0時,x≥

或x≤-1;當-2<a<0時,

≤x≤-1;
當a=-2時,x=-1;當a<-2時,-1≤x≤
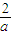
.
點評:本題考查不等式的解法,考查分類討論思想,是中檔題.
