【題目】已知設函數
.
（1）若
，求
極值；
（2）證明：當
，
時，函數在
上存在零點.
【答案】（1）
取得極大值0，無極小值（2）見證明
【解析】
（1）通過求導得到
，求出
的根，列表求出的單調區間和極值.
（2）對
進行分類，當
時，通過對求導，得到
在
單調遞減，找到其零點，進而得到的單調性，找到
，
，可證在
上存在零點.
當
時，根據（1）得到的結論，對進行放縮，得到
，再由，可證在上存在零點.
（1）當
時，
，定義域為
，由
得
．
當
變化時，， 的變化情況如下表：
|
|
|
|
|
|
|
|
|
| 極大值 |
|
故當時，取得極大值
，無極小值．
（2）
，
．
當
時，因
，所以
，
在單調遞減．
因為
，
，
所以有且僅有一個
，使
，
當
時，
，當
時，
，
所以
在
單調遞增，在
單調遞減．
所以
，而
，
所以在存在零點．
當
時，由（1）得
，
于是
，所以
．
所以
．
于是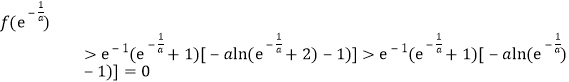
．
因為，所以所以在
存在零點．
綜上，當
，
時，函數在上存在零點．
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】
某位同學進行寒假社會實踐活動，為了對白天平均氣溫與某奶茶店的某種飲料銷量之間的關系進行分析研究，他分別記錄了1月11日至1月15日的白天平均氣溫
（°C）與該奶茶店的這種飲料銷量
（杯），得到如下數據：
日 期 | 1月11日 | 1月12日 | 1月13日 | 1月14日 | 1月15日 |
平均氣溫 | 9 | 10 | 12 | 11 | 8 |
銷量 | 23 | 25 | 30 | 26 | 21 |
（1）若從這五組數據中隨機抽出2組，求抽出的2組數據恰好是相鄰2天數據的概率；
（2）請根據所給五組數據，求出y關于x的線性回歸方程
．
（參考公式：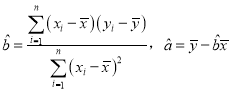
．）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，如圖所示，已知橢圓
的左、右頂點分別為
，
，右焦點為
.設過點
的直線
，
與此橢圓分別交于點
，
，其中
，
，
.
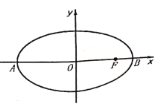
（1）設動點
滿足：
，求點的軌跡；
（2）設
，
，求點
的坐標；
（3）設
，求證：直線
必過
軸上的一定點（其坐標與
無關），并求出該定點的坐標.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】2018年10月28日，重慶公交車墜江事件震驚全國，也引發了廣大群眾的思考——如何做一個文明的乘客.全國各地大部分社區組織居民學習了文明乘車規范.
社區委員會針對居民的學習結果進行了相關的問卷調查，并將得到的分數整理成如圖所示的統計圖.
（Ⅰ）求得分在
上的頻率；
（Ⅱ）求社區居民問卷調查的平均得分的估計值；（同一組中的數據以這組數據所在區間中點的值作代表）
（Ⅲ）以頻率估計概率，若在全部參與學習的居民中隨機抽取5人參加問卷調查，記得分在
間的人數為
，求的分布列.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如上圖所示，在正方體
中， 
分別是棱
的中點， 
的頂點
在棱
與棱
上運動，有以下四個命題：
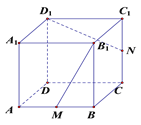
A．平面
； B．平面
⊥平面
；
C． 
在底面
上的射影圖形的面積為定值；
D． 
在側面
上的射影圖形是三角形．其中正確命題的序號是__________.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的左焦點在拋物線
的準線上，且橢圓的短軸長為2，
分別為橢圓的左，右焦點，
分別為橢圓的左，右頂點，設點
在第一象限，且
軸，連接
交橢圓于點
，直線的斜率為
.
（Ⅰ）求橢圓的方程；
（Ⅱ）若三角形
的面積等于四邊形
的面積，求的值；
（Ⅲ）設點
為
的中點，射線
（
為原點）與橢圓交于點
，滿足
，求的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
