
【題目】已知函數![]() .
.
(1)求函數![]() 的單調區間
的單調區間
(2)當![]() 時,求函數
時,求函數![]() 在
在![]() 上的最小值
上的最小值
【答案】(1) 當![]() 時,函數
時,函數![]() 的單調増區間為
的單調増區間為![]() ; 當
; 當![]() 時,函數
時,函數![]() 的單調遞增區間為
的單調遞增區間為![]() ,單調遞減區間為
,單調遞減區間為![]() ;(2) 當
;(2) 當![]() 時,函數
時,函數![]() 的最小值是
的最小值是![]() ;當
;當![]() 時,函數
時,函數![]() 的最小值是
的最小值是![]() .
.
【解析】試題分析:(1)首先對![]() 進行求導,然后分
進行求導,然后分![]() 與
與![]() 兩種情況討論,分別令
兩種情況討論,分別令![]() 求得
求得![]() 的范圍,可得函數
的范圍,可得函數![]() 增區間,
增區間, ![]() 求得
求得![]() 的范圍,可得函數
的范圍,可得函數![]() 的減區間;(2)結合(1)的結論,對
的減區間;(2)結合(1)的結論,對![]() 在
在![]() 三個區間進行討論,從而判斷其在區間[
三個區間進行討論,從而判斷其在區間[![]() 上單調性,根據單調性確定最小值.
上單調性,根據單調性確定最小值.
試題解析:(1)![]() ,
,
①當![]() 時,
時, ![]() ,即函數
,即函數![]() 的單調増區間為
的單調増區間為![]()
②當![]() 時,令
時,令![]() ,可得
,可得 ![]() ,
,
當![]() 時,
時, ![]() ;
;
當![]() 時,
時, ![]() ,故函數
,故函數![]() 的單調遞增區間為
的單調遞增區間為![]() ,單調遞減區間為
,單調遞減區間為![]() .
.
(2)①當![]() ,即
,即![]() 時,函數
時,函數![]() 在區間[
在區間[![]() 上是減函數,所以
上是減函數,所以![]() 的最小值是
的最小值是![]() .
.
②當![]() ,即
,即![]() 時,函數
時,函數![]() 在區間
在區間![]() 上是增函數,所以
上是增函數,所以![]() 的最小值是
的最小值是![]() .
.
③當![]() ,即
,即![]() 時,函數
時,函數![]() 在
在![]() 上是增函數,在
上是增函數,在![]() 上是減函數.
上是減函數.
又![]() ,
,
所以當![]() 時,最小值是
時,最小值是![]() ;
;
當![]() 時,最小值為
時,最小值為![]() .
.
綜上可知,
當![]() 時,函數
時,函數![]() 的最小值是
的最小值是![]() ;
;
當![]() 時,函數
時,函數![]() 的最小值是
的最小值是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】某公司計劃購買2臺機器,該種機器使用三年后即被淘汰.機器有一易損零件,在購進機器時,可以額外購買這種零件作為備件,每個200元.在機器使用期間,如果備件不足再購買,則每個500元.現需決策在購買機器時應同時購買幾個易損零件,為此搜集并整理了100臺這種機器在三年使用期內更換的易損零件數,得下面柱狀圖:

以這100臺機器更換的易損零件數的頻率代替1臺機器更換的易損零件數發生的概率,記X表示2臺機器三年內共需更換的易損零件數,n表示購買2臺機器的同時購買的易損零件數.
(1)求X的分布列;
(2)若要求P(X≤n)≤0.5,確定n的最小值;
(3)以購買易損零件所需費用的期望值為決策依據,在n=19與n=20之中選其一,應選用哪個?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來我國電子商務行業迎來發展的新機遇,2017年雙11全天交易額達到1682億元,為規范和評估該行業的情況,相關管理部門制定出針對電商的商品和服務的評價體系.現從評價系統中選出200次成功交易,并對其評價進行評價,對商品的好評率為0.6,對服務的好評率為0.75,其中對商品和服務都做出好評的交易為80次.
(1)完成關于商品和服務評價的![]() 列聯表,判斷能否在犯錯誤的概率不超過0.001的前提下,認為商品好評與服務好評有關?
列聯表,判斷能否在犯錯誤的概率不超過0.001的前提下,認為商品好評與服務好評有關?
(2)若將頻率視為概率,某人在該購物平臺上進行的3次購物中,設對商品和服務全為好評的次數為隨機變量![]() :
:
①求對商品和服務全為好評的次數![]() 的分布列;
的分布列;
②求![]() 的數學期望和方差.
的數學期望和方差.
附:臨界值表:

![]() 的觀測值:
的觀測值: 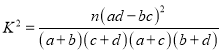 (其中
(其中![]() )
)
關于商品和服務評價的![]() 列聯表:
列聯表:

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2017·黃岡質檢)設等比數列{an}的各項均為正數,公比為q,前n項和為Sn.若對任意的n∈N*,有S2n<3Sn,則q的取值范圍是( )
A. (0,1] B. (0,2)
C. [1,2) D. (0, ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱柱![]() 中,
中, ![]() 平面
平面![]() ,底面
,底面![]() 為梯形,
為梯形, ![]() ,
, ![]() ,
, ![]() ,點
,點![]() ,
, ![]() 分別為
分別為![]() ,
, ![]() 的中點.
的中點.
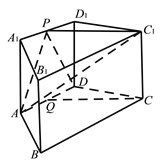
(Ⅰ)求證: ![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)在線段![]() 上是否存在點
上是否存在點![]() ,使
,使![]() 與平面
與平面![]() 所成角的正弦值是
所成角的正弦值是![]() ,若存在,求
,若存在,求![]() 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com