
【題目】給定一個n項的實數列![]() ,任意選取一個實數c,變換T(c)將數列a1,a2,…,an變換為數列|a1﹣c|,|a2﹣c|,…,|an﹣c|,再將得到的數列繼續實施這樣的變換,這樣的變換可以連續進行多次,并且每次所選擇的實數c可以不相同,第k(k∈N*)次變換記為Tk(ck),其中ck為第k次變換時選擇的實數.如果通過k次變換后,數列中的各項均為0,則稱T1(c1),T2(c2),…,Tk(ck)為“k次歸零變換”.
,任意選取一個實數c,變換T(c)將數列a1,a2,…,an變換為數列|a1﹣c|,|a2﹣c|,…,|an﹣c|,再將得到的數列繼續實施這樣的變換,這樣的變換可以連續進行多次,并且每次所選擇的實數c可以不相同,第k(k∈N*)次變換記為Tk(ck),其中ck為第k次變換時選擇的實數.如果通過k次變換后,數列中的各項均為0,則稱T1(c1),T2(c2),…,Tk(ck)為“k次歸零變換”.
(1)對數列:1,3,5,7,給出一個“k次歸零變換”,其中k≤4;
(2)證明:對任意n項數列,都存在“n次歸零變換”;
(3)對于數列1,22,33,…,nn,是否存在“n﹣1次歸零變換”?請說明理由.
【答案】(1)見解析(2)見解析(3)不存在,見解析
【解析】
(1)根據定義取恰當的值進行變換得解;
(2)結合(1)進行歸零變換的過程,可以考慮構造數列,經過k次變換后,數列記為![]() ,k=1,2,…,進行變換Tk(ck)時,
,k=1,2,…,進行變換Tk(ck)時,![]() ,依次變換即可得證;
,依次變換即可得證;
(3)利用數學歸納法證明該數列不存在“n﹣1次歸零變換”.
(1)方法1:T1(4):3,1,1,3;T2(2):1,1,1,1;T3(1):0,0,0,0.
方法2:T1(2):1,1,3,5;T2(2):1,1,1,3;T3(2):1,1,1,1;T4(1):0,0,0,0..…
(2)經過k次變換后,數列記為![]() ,k=1,2,….
,k=1,2,….
取![]() ,則
,則![]() ,即經T1(c1)后,前兩項相等;
,即經T1(c1)后,前兩項相等;
取![]() ,則
,則![]() ,即經T2(c2)后,前3項相等;
,即經T2(c2)后,前3項相等;
…
設進行變換Tk(ck)時,其中![]() ,變換后數列變為
,變換后數列變為![]() ,則
,則![]() ;
;
那么,進行第k+1次變換時,取![]() ,
,
則變換后數列變為![]() ,
,
顯然有![]() ;
;
…
經過n﹣1次變換后,顯然有![]() ;
;
最后,取![]() ,經過變換Tn(cn)后,數列各項均為0.
,經過變換Tn(cn)后,數列各項均為0.
所以對任意數列,都存在“n次歸零變換”.
(3)不存在“n﹣1次歸零變換”.
證明:首先,“歸零變換”過程中,若在其中進行某一次變換Tj(cj)時,cj<min{a1,a2,…,an},那么此變換次數便不是最少.這是因為,這次變換并不是最后的一次變換(因它并未使數列化為全零),設先進行Tj(cj)后,再進行Tj+1(cj+1),由||ai﹣cj|﹣cj+1|=|ai﹣(cj+cj+1)|,即等價于一次變換Tj(cj+cj+1),同理,進行某一步Tj(cj)時,cj>max{a1,a2,…,an};此變換步數也不是最小.
由以上分析可知,如果某一數列經最少的次數的“歸零變換”,每一步所取的ci滿足min{a1,a2,…,an}≤ci≤max{a1,a2,…,an}.
以下用數學歸納法來證明,對已給數列,不存在“n﹣1次歸零變換”.
(1)當n=2時,對于1,4,顯然不存在“一次歸零變換”,結論成立.
(由(2)可知,存在“兩次歸零變換”變換:![]() )
)
(2)假設n=k時成立,即1,22,33,…,kk不存在“k﹣1次歸零變換”.
當n=k+1時,假設1,22,33,…,kk,(k+1)k+1存在“k次歸零變換”.
此時,對1,22,33,…,kk也顯然是“k次歸零變換”,由歸納假設以及前面的討論不難知1,22,33,…,kk不存在“k﹣1次歸零變換”,則k是最少的變換次數,每一次變換ci一定滿足![]() ,i=1,2,…,k.
,i=1,2,…,k.
因為![]() (k+1)k+1﹣kkk>0
(k+1)k+1﹣kkk>0
所以,(k+1)k+1絕不可能變換為0,與歸納假設矛盾.
所以,當n=k+1時不存在“k次歸零變換”.
由(1)(2)命題得證.


科目:高中數學 來源: 題型:
【題目】下列關于命題的說法錯誤的是( )
A.命題“若x2﹣3x+2=0,則x=2”的逆否命題為“若x≠2,則x2﹣3x+2≠0”
B.“a=2”是“函數f(x)=ax在區間(﹣∞,+∞)上為增函數”的充分不必要條件
C.命題“x∈R,使得x2+x+1<0”的否定是:“x∈R,均有x2+x+1≥0”
D.“若f ′(![]() )=0,則
)=0,則![]() 為y=f(x)的極值點”為真命題
為y=f(x)的極值點”為真命題
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,以原點為圓心,橢圓
,以原點為圓心,橢圓![]() 的短半軸長為半徑的圓與直線
的短半軸長為半徑的圓與直線![]() 相切.
相切.
(Ⅰ)求橢圓方程;
(Ⅱ)設![]() 為橢圓右頂點,過橢圓
為橢圓右頂點,過橢圓![]() 的右焦點的直線
的右焦點的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
,![]() 兩點(異于
兩點(異于![]() ),直線
),直線![]() ,
,![]() 分別交直線
分別交直線![]() 于
于![]() ,
,![]() 兩點. 求證:
兩點. 求證:![]() ,
,![]() 兩點的縱坐標之積為定值.
兩點的縱坐標之積為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正三棱柱![]() 的所有棱長都為
的所有棱長都為![]() 是
是![]() 的中點,
的中點,![]() 在
在![]() 邊上,
邊上,![]() .
.
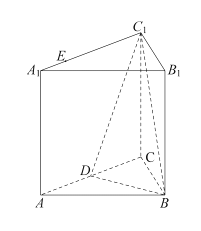
(1)證明:平面![]() 平面
平面![]() ;
;
(2)若![]() 是側面
是側面![]() 內的動點,且
內的動點,且![]() 平面
平面![]() .
.
①在答題卡中作出點![]() 的軌跡,并說明軌跡的形狀(不需要說明理由);
的軌跡,并說明軌跡的形狀(不需要說明理由);
②求二面角![]() 的余弦值的最大值.
的余弦值的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C所對的邊分別為a,b,c,且acosC+ccosA=2bcosA.
(1)求角A的值;
(2)若![]() ,
, ![]() ,求△ABC的面積S.
,求△ABC的面積S.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設min{m,n}表示m,n二者中較小的一個,已知函數f(x)=x2+8x+14,g(x)=![]() (x>0),若x1∈[-5,a](a≥-4),x2∈(0,+∞),使得f(x1)=g(x2)成立,則a的最大值為
(x>0),若x1∈[-5,a](a≥-4),x2∈(0,+∞),使得f(x1)=g(x2)成立,則a的最大值為
A.-4B.-3C.-2D.0
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com