【題目】已知函數
為奇函數.
（1）求實數
的值；
（2）用定義法討論并證明函數
的單調性.
【答案】（1）
（2）
在定義域
上為減函數，證明見解析
【解析】
(1)根據奇函數的定義
，得出
，化簡得到
，從而得到
或1，再判斷函數定義域是否關于原點對稱，即可確定實數
的值；
(2) 令
，利用作差法比較
，
的大小，再根據對數函數的單調性得
，即
，結合函數單調性的定義，即可判斷函數
的單調性.
解：（1）由
及函數為奇函數可知，
有，得
有
，得
，得，故有或1，
①當時，
，此時函數定義域為
，不關于原點對稱，不可能是奇函數，
②當時，
，令
，可得
，故此時函數的定義域為
關于原點對稱，函數為奇函數.
由上知.
（2）由（1）知
，
令，有
，
∵，
∴
，
，
，
∴
，可得
，即
，
利用對數函數的單調性得，即，
故函數在定義域上為減函數.
科目：高中數學 來源： 題型：
【題目】給定空間中十個點，其中任意四點不在一個平面上，將某些點之間用線段相連，若得到的圖形中沒有三角形也沒有空間四邊形，試確定所連線段數目的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在底面半徑為6的圓柱內，有兩個半徑也為6的球面，兩球的球心距為13，若作一個平面與兩個球都相切，且與圓柱面相交成一橢圓，則橢圓的長軸長為 ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖為某大河的一段支流，岸線
近似滿足
∥
寬度為7
圓
為河中的一個半徑為2
的小島，小鎮
位于岸線上，且滿足岸線
現計劃建造一條自小鎮經小島至對岸
的通道
（圖中粗線部分折線段，
在右側），為保護小島，
段設計成與圓相切，設
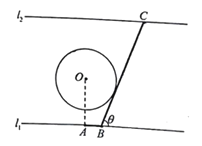
（1）試將通道的長
表示成
的函數，并指出其定義域.
（2）求通道的最短長.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在抗擊新型冠狀病毒肺炎期間，為響應政府號召，郴州市某單位組織了志愿者30人，其中男志愿者18人，用分層抽樣的方法從該單位志愿者中抽取5人去參加某社區的防疫幫扶活動．
（1）求從該單位男、女志愿者中各抽取的人數；
（2）從抽取的5名志愿者中任選2名談此活動的感受，求選出的2名志愿者中恰有1名男志愿者的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】正四棱錐
的底面正方形邊長是3，
是在底面上的射影，
，
是
上的一點，過且與
、
都平行的截面為五邊形
．
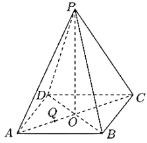
（1）在圖中作出截面，并寫出作圖過程；
（2）求該截面面積的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知袋子中放有大小和形狀相同的小球若干，其中標號為0的小球1個，標號為1的小球1個，標號為2的小球
個.若從袋子中隨機抽取1個小球，取到標號為2的小球的概率是
.
（1）求的值；
（2）從袋子中不放回地隨機抽取2個小球，記第一次取出的小球標號為
，第二次取出的小球標號為
.
①記“
”為事件
，求事件的概率；
②在區間
內任取2個實數
，
，求事件“
恒成立”的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】將函數y=2cos（2x+
）的圖象向左平移
個單位長度，得到函數y=f（x）的圖象．
（1）求f（x）的單調遞增區間；
（2）求f（x）在[0，
]上的值域．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f(x)＝
x3－2x2＋3x(x∈R)的圖象為曲線C.
(1)求過曲線C上任意一點切線斜率的取值范圍；
(2)若在曲線C上存在兩條相互垂直的切線，求其中一條切線與曲線C的切點的橫坐標的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com