
【題目】下列各種情況下,向量終點構成什么圖形?
(1)把所有單位向量的起點平移到同一點![]() ;
;
(2)把平行于某一直線的所有單位向量的起點平移到同一點;
(3)把平行于某一直線的一切向量平移到同一起點.
科目:高中數學 來源: 題型:
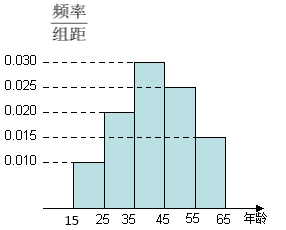
【題目】某網絡營銷部門為了統計某市網友“雙11”在某淘寶店的網購情況,隨機抽查了該市當天60名網友的網購金額情況,得到如下數據統計表(如圖):

若網購金額超過2千元的顧客定義為“網購達人”,網購金額不超過2千元的顧客定義為“非網購達人”,已知“非網購達人”與“網購達人”人數比恰好為3:2.
(1)試確定![]() 的值,并補全頻率分布直方圖;
的值,并補全頻率分布直方圖;
(2)試營銷部門為了進一步了解這60名網友的購物體驗,從“非網購達人”、“網購達人”中用分層抽樣的方法確定5人,若需從這5人中隨機選取2人進行問卷調查,則恰好選取1名“網購達人”和1名“非網購達人”的概率是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著節假日外出旅游人數增多,倡導文明旅游的同時,生活垃圾處理也面臨新的挑戰,某海濱城市沿海有![]() 三個旅游景點,在岸邊
三個旅游景點,在岸邊![]() 兩地的中點處設有一個垃圾回收站點
兩地的中點處設有一個垃圾回收站點![]() (如圖),
(如圖),![]() 兩地相距10
兩地相距10![]() ,從回收站
,從回收站![]() 觀望
觀望![]() 地和
地和![]() 地所成的視角為
地所成的視角為![]() ,且
,且![]() ,設
,設![]() ;
;
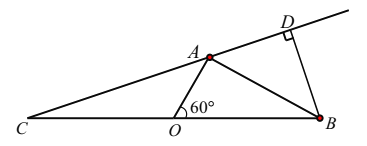
(1)用![]() 分別表示
分別表示![]() 和
和![]() ,并求出
,并求出![]() 的取值范圍;
的取值范圍;
(2)某一時刻太陽與![]() 三點在同一直線,此時
三點在同一直線,此時![]() 地到直線
地到直線![]() 的距離為
的距離為![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 與曲線
與曲線![]() 有三個不同的交點.
有三個不同的交點.
(1)求圓![]() 的方程;
的方程;
(2)已知點![]() 是
是![]() 軸上的動點,
軸上的動點, ![]() ,
, ![]() 分別切圓
分別切圓![]() 于
于![]() ,
, ![]() 兩點.
兩點.
①若![]() ,求
,求![]() 及直線
及直線![]() 的方程;
的方程;
②求證:直線![]() 恒過定點.
恒過定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4—1:幾何證明選講
如圖,已知AP是⊙O的切線,P為切點,AC是⊙O的割線,與⊙O交于B、C兩點,圓心O在∠PAC的內部,點M是BC的中點.
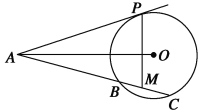
(1)證明:A、P、O、M四點共圓;
(2)求∠OAM+∠APM的大小
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,直三棱柱ABC-A1B1C1底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2M,N分別是A1B1,A1A的中點。
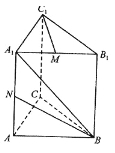
(1)求![]() 的長度;
的長度;
(2)求cos(![]() ,
,![]() )的值;
)的值;
(3)求證:A1B⊥C1M。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了了解我國各景點在大眾中的熟知度,隨機對![]() ~
~![]() 歲的人群抽樣了
歲的人群抽樣了![]() 人,回答問題“我國的“五岳”指的是哪五座名山?”統計結果如下圖表.
人,回答問題“我國的“五岳”指的是哪五座名山?”統計結果如下圖表.
組號 | 分組 | 回答正確的人數 | 回答正確的人數占本組的頻率 |
第1組 | [15,25) |
| 0.5 |
第2組 | [25,35) | 18 |
|
第3組[ | [35,45) |
| 0.9 |
第4組 | [45,55) | 9 | 0.36 |
第5組 | [55,65] | 3 |
|
![]()
(1)分別求出![]() 的值;
的值;
(2)從第![]() 組回答正確的人中用分層抽樣的方法抽取
組回答正確的人中用分層抽樣的方法抽取![]() 人,求第
人,求第![]() 組每組各抽取多少人;
組每組各抽取多少人;
(3)在(2)的條件下抽取的![]() 人中,隨機抽取
人中,隨機抽取![]() 人,求所抽取的人中恰好沒有第
人,求所抽取的人中恰好沒有第![]() 組人的概率.
組人的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列命題:
①已知集合![]() ,則“
,則“![]() ”是“
”是“![]() ”的充分不必要條件;
”的充分不必要條件;
②“![]() ”是“
”是“![]() ”的必要不充分條件;
”的必要不充分條件;
③“函數![]() 的最小正周期為
的最小正周期為![]() ”是“
”是“![]() ”的充要條件;
”的充要條件;
④“平面向量![]() 與
與![]() 的夾角是鈍角”的要條件是“
的夾角是鈍角”的要條件是“![]() ”.
”.
其中正確命題的序號是 .(把所有正確命題的序號都寫上)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com