已知函數(shù)
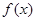
滿足對一切
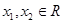
都有
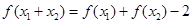
,且
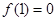
,當
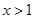
時有
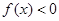
.
(1)求
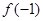
的值;
(2)判斷并證明函數(shù)
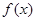
在
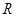
上的單調(diào)性;
(3)解不等式:
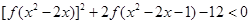
.
(1)
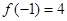
(2)利用函數(shù)的定義法來證明函數(shù)單調(diào)性,注意設(shè)變量的任意性,以及作差法,變形定號,下結(jié)論的步驟。
(3)
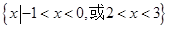
試題分析:解:⑴令
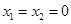
,得
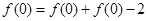
,
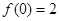
再令
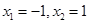
,得
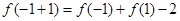
,
即
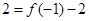
,從而
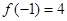
. 2分
⑵任取
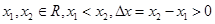
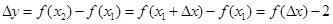
4分
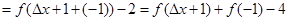
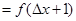
.
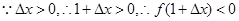
,即
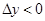
.

在
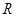
上是減函數(shù). 6分
⑶由條件知,
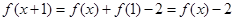
,
設(shè)
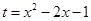
,則
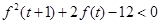
,即
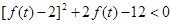
,
整理,得
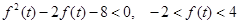
, 8分
而
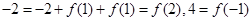
,
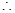
不等式即為
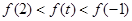
,
又因為
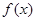
在
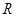
上是減函數(shù),
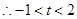
,即
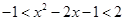
, 10分
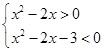
,從而所求不等式的解集為
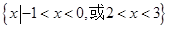
. 12分
點評:解決的關(guān)鍵是利用賦值法思想求值,同時借助于函數(shù)單調(diào)性定義證明單調(diào)性,從而解不等式。屬于基礎(chǔ)題。
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
已知
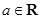
,函數(shù)
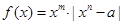
.
(1)若
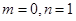
,寫出函數(shù)
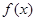
的單調(diào)遞增區(qū)間(不必證明);
(2)若
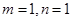
,當
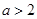
時,求函數(shù)
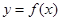
在區(qū)間
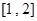
上的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
已知
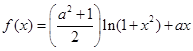

.
(1)
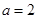
時,求
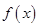
的極值;
(2)當
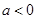
時,討論
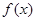
的單調(diào)性;
(3)證明:
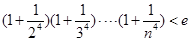
(
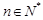
,
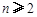
,其中無理數(shù)
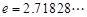
)
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
函數(shù)
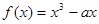
在
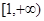
上是單調(diào)遞增函數(shù),則
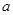
的取值范圍是_____________。
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
函數(shù)
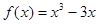
的遞減區(qū)間是
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
已知函數(shù)
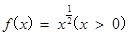
,若對于任意
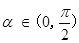
,都有
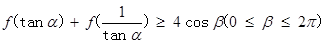
成立,則
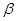
的取值范圍是
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
已知函數(shù)
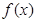
(
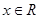
)滿足
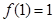
,且
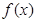
的導(dǎo)函數(shù)
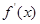
<
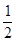
,則
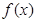
<
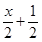
的解集為( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
證明函數(shù)f(x)=x+
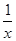
在(0,1)上是減函數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
(12分)已知
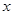
滿足
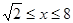
,求函數(shù)
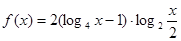
的最大值和最小值
查看答案和解析>>

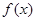 滿足對一切
滿足對一切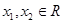 都有
都有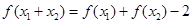 ,且
,且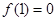 ,當
,當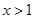 時有
時有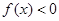 .
.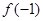 的值;
的值;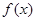 在
在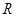 上的單調(diào)性;
上的單調(diào)性;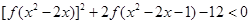 .
. 云南師大附小一線名師提優(yōu)作業(yè)系列答案
云南師大附小一線名師提優(yōu)作業(yè)系列答案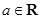 ,函數(shù)
,函數(shù)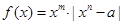 .
.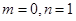 ,寫出函數(shù)
,寫出函數(shù)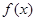 的單調(diào)遞增區(qū)間(不必證明);
的單調(diào)遞增區(qū)間(不必證明);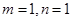 ,當
,當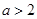 時,求函數(shù)
時,求函數(shù)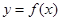 在區(qū)間
在區(qū)間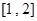 上的最小值.
上的最小值.