【題目】十九世紀末：法國學者貝特朗在研究幾何概型時提出了“貝特朗悖論”，即“在一個圓內任意選一條弦，這條弦的弦長長于這個圓的內接等邊三角形邊長的概率是多少？”貝特朗用“隨機半徑”“隨機端點”“隨機中點”三個合理的求解方法，但結果都不相同．該悖論的矛頭直擊概率概念本身，強烈地刺激了概率論基礎的嚴格化．已知“隨機端點”的方法如下：設
為圓
上一個定點，在圓周上隨機取一點
，連接
，所得弦長大于圓的內接等邊三角形邊長的概率．則由“隨機端點”求法所求得的概率為（ ）
A.
B.
C.
D.
口算題天天練系列答案科目：高中數學 來源： 題型：
【題目】定義：對于任意
，滿足條件
且
是與
無關的常數
的無窮數列
稱為
數列．
（1）若
，證明：數列是數列；
（2）設數列
的通項為
，且數列是數列，求常數
的取值范圍；
（3）設數列
，問數列是否是數列？請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，在四棱錐
中，四邊形
為矩形， 
為等腰三角形， 
，平面
平面
，且
， 
， 
分別為
的中點.
（1）證明： 
平面
；
（2）證明：平面
平面
；
（3）求四棱錐
的體積.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】“90后”指1990年及以后出生，“80后”指1980-1989年之間出生，“80前”指1979年及以前出生.某調查機構對全國互聯網行業進行調查統計，得到整個互聯網行業從業者年齡分布餅狀圖、90后從事互聯網行業崗位分布條形圖，則下列結論中不一定正確的是（ ）
A.互聯網行業從業人員中90后占一半以上
B.互聯網行業中從事技術崗位的人數超過總人數的
C.互聯網行業中從事運營崗位的人數90后比80前多
D.互聯網行業中從事技術崗位的人數90后比80后多
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】定義：若數列
中存在
，其中
，
，
，
，
及
均為正整數，且
（
），則稱數列為“
數列”.
（1）若數列
的前
項和
，求證：是“數列”；
（2）若
是首項為1，公比為
的等比數列，判斷是否是“數列”，說明理由；
（3）若
是公差為
（
）的等差數列且
（
），
，求證：數列是“數列”.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在實數集R中，我們定義的大小關系“＞”為全體實數排了一個“序”．類似的，我們在平面向量集
上也可以定義一個稱“序”的關系，記為“
”．定義如下：對于任意兩個向量
，“
”當且僅當“
”或“
”。按上述定義的關系“”，給出如下四個命題：
①若
，則
；
②若
，則
；
③若，則對于任意
；
④對于任意向量
，若，則
。
其中真命題的序號為__________
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（本題滿分12分） 如圖，
的外接圓
的半徑為
，
所在的平面，
，
，
，且
，
．
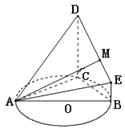
（1）求證：平面ADC
平面BCDE．
（2）試問線段DE上是否存在點M，使得直線AM與平面ACD所成角的正弦值為
？若存在，
確定點M的位置，若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列命題錯誤的是（ ）
A. 命題“若
，則
”的逆否命題為“若
，則
”
B. 若
為假命題，則
均為假命題
C. 對于命題
：
，使得
，則
：
，均有
D. “
”是“
”的充分不必要條件
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
