
【題目】已知雙曲線![]() 的兩焦點為
的兩焦點為![]() ,
,![]() 為動點,若
為動點,若![]() .
.
(1)求動點![]() 的軌跡
的軌跡![]() 方程;
方程;
(2)若![]() ,設直線
,設直線![]() 過點
過點![]() ,且與軌跡
,且與軌跡![]() 交于
交于![]() 兩點,直線
兩點,直線![]() 與
與![]() 交于
交于![]() 點.試問:當直線
點.試問:當直線![]() 在變化時,點
在變化時,點![]() 是否恒在一條定直線上?若是,請寫出這條定直線方程,并證明你的結論;若不是,請說明理由.
是否恒在一條定直線上?若是,請寫出這條定直線方程,并證明你的結論;若不是,請說明理由.
【答案】(1)![]() ;(2)是,
;(2)是,![]()
【解析】
(1)根據![]() ,且
,且![]() ,由橢圓的定義可知,動點
,由橢圓的定義可知,動點![]() 的軌跡是以
的軌跡是以![]() 為焦點的橢圓,再求出
為焦點的橢圓,再求出![]() ,寫出方程.
,寫出方程.
(2)先設直線的方程為![]() ,如果存在,則對任意
,如果存在,則對任意![]() 都成立,首先取特殊情況,當
都成立,首先取特殊情況,當![]() 時,探究出該直線為
時,探究出該直線為![]() ,再通過一般性的證明即可.
,再通過一般性的證明即可.
(1)雙曲線![]() 的兩焦點為
的兩焦點為![]() ,
,
設動點![]()
![]() ,
,
因為![]() ,且
,且![]() ,
,
所以動點![]() 的軌跡
的軌跡![]() 是以
是以![]() 為焦點的橢圓.
為焦點的橢圓.
因為![]() ,
,
所以的軌跡![]() 方程;
方程;![]() .
.
(2)由題意設直線的方程為![]() ,
,
取![]() ,得
,得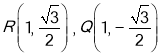 ,
,
直線![]() 的方程是
的方程是![]() ,
,
直線![]() 的方程是
的方程是![]() ,
,
交點為![]() .
.
若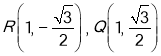 ,由對稱性可知:交點為
,由對稱性可知:交點為![]() .
.
若點![]() 在同一條直線上,則該直線只能為
在同一條直線上,則該直線只能為![]() .
.
以下證明 對任意的![]() ,直線
,直線![]() 與
與![]() 交點
交點![]() 均在直線
均在直線![]() 上.
上.
由 得
得![]() ,
,
設![]() ,
,
由韋達定理得:![]()
設直線![]() 與
與![]() 交點為
交點為![]() ,
,
由![]() ,
,
得![]() .
.
設直線![]() 與
與![]() 交點為
交點為![]() ,
,
由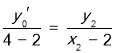 ,
,
得![]() ,
,
因為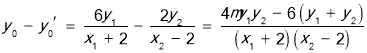 ,
,
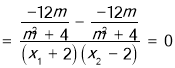 .
.
所以![]() 與
與![]() 重合.
重合.
所以當直線![]() 在變化時,點
在變化時,點![]() 恒在直線
恒在直線![]() 上.
上.


科目:高中數學 來源: 題型:
【題目】有![]() 名學生排成一排,求分別滿足下列條件的排法種數,要求列式并給出計算結果.
名學生排成一排,求分別滿足下列條件的排法種數,要求列式并給出計算結果.
(1)甲不在兩端;
(2)甲、乙相鄰;
(3)甲、乙、丙三人兩兩不得相鄰;
(4)甲不在排頭,乙不在排尾。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 的前
的前![]() 項和為
項和為![]() .數列
.數列![]() 滿足
滿足![]() ,
,![]() .
.
(1)若![]() ,且
,且![]() ,求正整數
,求正整數![]() 的值;
的值;
(2)若數列![]() ,
,![]() 均是等差數列,求
均是等差數列,求![]() 的取值范圍;
的取值范圍;
(3)若數列![]() 是等比數列,公比為
是等比數列,公比為![]() ,且
,且![]() ,是否存在正整數
,是否存在正整數![]() ,使
,使![]() ,
,![]() ,
,![]() 成等差數列,若存在,求出一個
成等差數列,若存在,求出一個![]() 的值,若不存在,請說明理由.
的值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解人們對“延遲退休年齡政策”的態度,某部門從年齡在15歲到65歲的人群中隨機調查了100人,將這100人的年齡數據分成5組:![]()
![]()
![]()
![]()
![]() ,整理得到如圖所示的頻率分布直方圖.
,整理得到如圖所示的頻率分布直方圖.
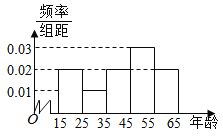
(1)由頻率分布直方圖,計算出各年齡段的人數,并估計這100人年齡的眾數、中位數和平均數;(該小題不用寫解題過程,請在答題卷上直接寫出答案
(2)支持“延遲退休”的人數如下表所示,根據以上統計數據填寫下面的2×2列聯表,據此表,能否有95%的把握認為以45歲為分界點的不同人群對“延遲退休年齡政”的不支持態度存在差異?
附: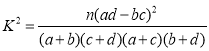 ,其中
,其中![]() .
.
年齡 |
|
|
|
|
|
支持“延遲退休”的人數 | 15 | 5 | 15 | 28 | 17 |
參考數據:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 分別是橢圓
分別是橢圓![]() 的左、右焦點.
的左、右焦點.
(1)若![]() 是該橢圓上的一個動點,求
是該橢圓上的一個動點,求![]() 的最大值和最小值;
的最大值和最小值;
(2)設過定點![]() 的直線
的直線![]() 與橢圓交于不同的兩點
與橢圓交于不同的兩點![]() ,且
,且![]() 為銳角(其中
為銳角(其中![]() 為坐標原點),求直線
為坐標原點),求直線![]() 的斜率的取值范圍.
的斜率的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2016年1月6日北京時間上午11時30分,朝鮮中央電視臺宣布“成功進行了氫彈試驗”,再次震動世界,此事件也引起了我國公民熱議,其中丹東市(丹東市和朝鮮隔江)某![]() 聊天群有300名網友,烏魯木齊市某微信群有200名網友,為了解不同地區我國公民對“氫彈試驗”事件的關注程度,現采用分層抽樣的方法,從中抽取了100名網友,先分別統計了他們在某時段發表的信息條數,再將兩地網友發表的信息條數分成5組:
聊天群有300名網友,烏魯木齊市某微信群有200名網友,為了解不同地區我國公民對“氫彈試驗”事件的關注程度,現采用分層抽樣的方法,從中抽取了100名網友,先分別統計了他們在某時段發表的信息條數,再將兩地網友發表的信息條數分成5組:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,分別加以統計,得到如圖所示的頻率分布直方圖.
,分別加以統計,得到如圖所示的頻率分布直方圖.
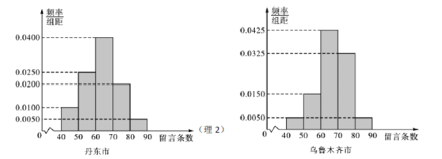
(1)求丹東市網友的平均留言條數(保留整數);
(2)為了進一步開展調查,從樣本中留言條數不足50條的網友中隨機抽取2人,求至少抽到一名烏魯木齊市網友的概率;
(3)規定“留言條數”不少于70條為“強烈關注”.
①請你根據已知條件完成下列![]() 的列聯表:
的列聯表:
強烈關注 | 非強烈關注 | 合計 | |
丹東市 | |||
烏魯木齊市 | |||
合計 |
②判斷是否有![]() 的把握認為“強烈關注”與網友所在的地區有關?
的把握認為“強烈關注”與網友所在的地區有關?
附:臨界值表及參考公式:
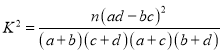 ,
,![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com