
分析 聯立方程組$\left\{\begin{array}{l}{y={x}^{2}+mx+2}\\{y=x+1}\end{array}\right.$,得x2+(m-1)x+1=0,由A∩B≠∅,將題目中的問題轉化為方程x2+(m-1)x+1=0在R內有解.由此能求出實數m的取值范圍.
解答 解:∵集合A={(x,y)|y=x2+mx+2},B={(x,y)|y=x+1},
∴聯立方程組$\left\{\begin{array}{l}{y={x}^{2}+mx+2}\\{y=x+1}\end{array}\right.$,
消去y得x2+(m-1)x+1=0,
∵A∩B≠∅,
∴將題目中的問題轉化為方程x2+(m-1)x+1=0在R內有解.
∴△=(m-1)2-4≥0,
解得m≥3或m≤-1,
∴實數m的取值范圍為:{m|m≥3或m≤-1}.
故答案為:{m|m≥3或m≤-1}.
點評 本題考查實數的取值范圍的求法,是基礎題,解題時要認真審題,注意等價轉化思想的合理運用.


 通城學典默寫能手系列答案
通城學典默寫能手系列答案科目:高中數學 來源: 題型:解答題
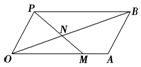 如圖所示,四邊形OABP是平行四邊形,過點P的直線與射線OA,OB分別相交于點M,N,若$\overrightarrow{OM}$=x$\overrightarrow{OA}$,$\overrightarrow{ON}$=y$\overrightarrow{OB}$.
如圖所示,四邊形OABP是平行四邊形,過點P的直線與射線OA,OB分別相交于點M,N,若$\overrightarrow{OM}$=x$\overrightarrow{OA}$,$\overrightarrow{ON}$=y$\overrightarrow{OB}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | y=x2 | B. | y=$\sqrt{x}$ | C. | y=log2x | D. | y=($\frac{1}{2}$)|x| |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{12}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (0,$\frac{3}{2}$) | B. | ($\frac{3}{2}$,0) | C. | (0,$\frac{1}{24}$) | D. | ($\frac{1}{24}$,0) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $({\frac{{5\sqrt{3}}}{2},\frac{3}{2}})$或 $({-\frac{{5\sqrt{3}}}{2},\frac{3}{2}})$ | B. | $({\frac{5}{2},\frac{{3\sqrt{3}}}{2}})$或$({\frac{5}{2},-\frac{{3\sqrt{3}}}{2}})$ | ||
| C. | (5,0)或(-5,0) | D. | (0,3)或(0,-3) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com