
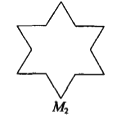
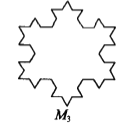
【題目】如圖☆的曲線,其生成方法是(I)將正三角形(圖(1))的每邊三等分,并以中間的那一條線段為一底邊向形外作等邊三角形,然后去掉底邊,得到圖(2);(II)將圖(2)的每邊三等分,重復上述的作圖方法,得到圖(3);(III)再按上述方法繼續做下去,所得到的曲線稱為雪花曲線(Koch Snowflake),
![]()
 (1)
(1) (2)
(2) (3)
(3) .
.
設圖(1)的等邊三角形的邊長為1,并且分別將圖(1)、(2)、(3)…中的圖形依次記作M1、M2、M3、…![]() …
…
(1)設![]() 中的邊數為
中的邊數為![]() 中每條邊的長度為
中每條邊的長度為![]() ,寫出數列
,寫出數列![]() 和
和![]() 的遞推公式與通項公式;
的遞推公式與通項公式;
(2)設![]() 的周長為
的周長為![]() ,
,![]() 所圍成的面積為
所圍成的面積為![]() ,求數列{
,求數列{![]() }與{
}與{![]() }的通項公式;請問周長
}的通項公式;請問周長![]() 與面積
與面積![]() 的極限是否存在?若存在,求出該極限,若不存在,簡單說明理由.
的極限是否存在?若存在,求出該極限,若不存在,簡單說明理由.
【答案】(1)![]() 且
且![]() ,
,![]() ;
;![]() ,
,![]() ; (2)
; (2)![]() ;
;![]() ;周長
;周長![]() 的極限不存在,面積
的極限不存在,面積![]() 的極限為
的極限為![]() .
.
【解析】
(1)根據題意,結合圖形的變換,分別得出數列![]() 和
和![]() 的遞推關系式,結合等比數列的通項公式,即可求解;
的遞推關系式,結合等比數列的通項公式,即可求解;
(2)根據圖象的變換規律,得出數列![]() 和
和![]() 的遞推關系式,結合疊加法和數列的極限,即可求解.
的遞推關系式,結合疊加法和數列的極限,即可求解.
(1)由題意,可得數列![]() 的遞推關系式為
的遞推關系式為![]() 且
且![]() ,
,
所以數列![]() 構成首項為
構成首項為![]() ,公比為4的等比數列,
,公比為4的等比數列,
所以其通項公式為![]() ,
,
又由每個圖形的邊長都相等,且長度變為原來的![]() ,
,
所以邊長![]() 滿足遞推關系式
滿足遞推關系式![]() ,
,
即數列![]() 構成首項為1,公比為
構成首項為1,公比為![]() 的等比數列,
的等比數列,
所以數列![]() 的圖通項公式為
的圖通項公式為![]()
(2)觀察發現,第二個圖形在第一個圖形的周長的基礎上多了它的周長的![]() ,第三個圖形在第二個的周長的基礎上,多了周長的
,第三個圖形在第二個的周長的基礎上,多了周長的![]() ,第四個圖形在第三個的周長的基礎上,多了周長的
,第四個圖形在第三個的周長的基礎上,多了周長的![]() ,依次類推,
,依次類推,
可得周長![]() 滿足遞推關系式
滿足遞推關系式![]() 且
且![]() ,
,
所以數列![]() 構成首項為3,公比為
構成首項為3,公比為![]() 的等比數列,
的等比數列,
所以數列![]() 的通項公式為
的通項公式為![]() ,
,
由第一個三角形的面積![]() ,
,
當![]() 時,
時,![]() ,
,
則![]()
 .
.
又由極限的運算法則,可得![]() ,所以周長
,所以周長![]() 的極限不存在;
的極限不存在;
![]() ,即面積
,即面積![]() 的極限為
的極限為![]() .
.


 小學課堂作業系列答案
小學課堂作業系列答案 金博士一點全通系列答案
金博士一點全通系列答案科目:高中數學 來源: 題型:
【題目】已知![]() ,
, ![]() 表示兩條不同的直線,
表示兩條不同的直線, ![]() ,
, ![]() ,
, ![]() 表示三個不同的平面,給出下列四個命題:
表示三個不同的平面,給出下列四個命題:
①![]() ,
, ![]() ,
, ![]() ,則
,則![]() ;
;
②![]() ,
, ![]() ,
, ![]() ,則
,則![]() ;
;
③![]() ,
, ![]() ,
, ![]() ,則
,則![]() ;
;
④![]() ,
, ![]() ,
, ![]() ,則
,則![]()
其中正確命題的序號為( )
A. ①② B. ②③ C. ③④ D. ②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() 的離心率為
的離心率為![]() ,橢圓
,橢圓![]() 上一點
上一點![]() 到左右兩個焦點
到左右兩個焦點![]() 的距離之和是4.
的距離之和是4.
(1)求橢圓的方程;
(2)已知過![]() 的直線與橢圓
的直線與橢圓![]() 交于
交于![]() 兩點,且兩點與左右頂點不重合,若
兩點,且兩點與左右頂點不重合,若![]() ,求四邊形
,求四邊形![]() 面積的最大值。
面積的最大值。
查看答案和解析>>
科目:高中數學 來源: 題型:
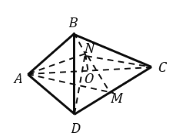
【題目】已知正方形![]() 的邊長為
的邊長為![]() ,將
,將![]() 沿對角線
沿對角線![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,得到如圖所示的三棱錐
,得到如圖所示的三棱錐![]() ,若
,若![]() 為
為![]() 邊的中點,
邊的中點,![]() 分別為
分別為![]() 上的動點(不包括端點),且
上的動點(不包括端點),且![]() ,設
,設![]() ,則三棱錐
,則三棱錐![]() 的體積取得最大值時,三棱錐
的體積取得最大值時,三棱錐![]() 的內切球的半徑為_______.
的內切球的半徑為_______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若對滿足條件3x+3y+8=2xy(x>0,y>0)的任意x、y,(x+y)2﹣a(x+y)+16≥0恒成立,則實數a的取值范圍是( )
A.(﹣∞,8]B.[8,+∞)C.(﹣∞,10]D.[10,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知五邊形ABECD由一個直角梯形ABCD與一個等邊三角形BCE構成,如圖1所示,AB丄BC,AB//CD,且AB=2CD。將梯形ABCD沿著BC折起,如圖2所示,且AB丄平面BEC。
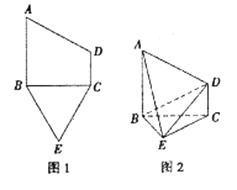
(1)求證:平面ABE丄平面ADE;
(2)若AB=BC,求二面角A-DE-B的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com