
【題目】已知函數f(x)=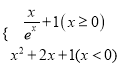 ,若函數y=f(f(x)﹣a)﹣1有三個零點,則a的取值范圍是_____.
,若函數y=f(f(x)﹣a)﹣1有三個零點,則a的取值范圍是_____.
【答案】![]()
【解析】當x<0時,由f(x)﹣1=0得x2+2x+1=1,得x=﹣2或x=0,
當x≥0時,由f(x)﹣1=0得![]() ,得x=0,
,得x=0,
由,y=f(f(x)﹣a)﹣1=0得f(x)﹣a=0或f(x)﹣a=﹣2,
即f(x)=a,f(x)=a﹣2,
作出函數f(x)的圖象如圖:
y=![]() ≥1(x≥0),
≥1(x≥0),
y′=![]() ,當x∈(0,1)時,y′>0,函數是增函數,x∈(1,+∞)時,y′<0,函數是減函數,
,當x∈(0,1)時,y′>0,函數是增函數,x∈(1,+∞)時,y′<0,函數是減函數,
x=1時,函數取得最大值: ![]() ,
,
當1<a﹣2![]() 時,即a∈(3,3+
時,即a∈(3,3+![]() )時,y=f(f(x)﹣a)﹣1有4個零點,
)時,y=f(f(x)﹣a)﹣1有4個零點,
當a﹣2=1+![]() 時,即a=3+
時,即a=3+![]() 時則y=f(f(x)﹣a)﹣1有三個零點,
時則y=f(f(x)﹣a)﹣1有三個零點,
當a>3+![]() 時,y=f(f(x)﹣a)﹣1有1個零點
時,y=f(f(x)﹣a)﹣1有1個零點
當a=1+![]() 時,則y=f(f(x)﹣a)﹣1有三個零點,
時,則y=f(f(x)﹣a)﹣1有三個零點,
當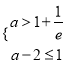 時,即a∈(1+
時,即a∈(1+![]() ,3)時,y=f(f(x)﹣a)﹣1有三個零點.
,3)時,y=f(f(x)﹣a)﹣1有三個零點.
綜上a∈![]() ,函數有3個零點.
,函數有3個零點.
故答案為: ![]() .
.


科目:高中數學 來源: 題型:
【題目】已知函數y=x+ ![]() (a>0)在區間
(a>0)在區間 ![]() 上單調遞減,在區間
上單調遞減,在區間 ![]() 上單調遞增;函數
上單調遞增;函數 ![]()
(1)請寫出函數f(x)=x2+ ![]() (a>0)與函數g(x)=xn+
(a>0)與函數g(x)=xn+ ![]() (a>0,n∈N,n≥3)在(0,+∞)的單調區間(只寫結論,不證明);
(a>0,n∈N,n≥3)在(0,+∞)的單調區間(只寫結論,不證明);
(2)求函數h(x)的最值;
(3)討論方程h2(x)﹣3mh(x)+2m2=0(0<m≤30)實根的個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,矩形ABCD是某小區戶外活動空地的平面示意圖,其中AB=50![]() 米,AD=100米,現擬在直角三角形OMN內栽植草坪供兒童踢球娛樂(其中,點O為AD的中點,OM⊥ON,點M在AB上,點N在CD上),將破舊的道路AM重新鋪設.已知草坪成本為每平方米20元,新道路AM成本為每米500元,設∠OMA=θ,記草坪栽植與新道路鋪設所需的總費用為f(θ).
米,AD=100米,現擬在直角三角形OMN內栽植草坪供兒童踢球娛樂(其中,點O為AD的中點,OM⊥ON,點M在AB上,點N在CD上),將破舊的道路AM重新鋪設.已知草坪成本為每平方米20元,新道路AM成本為每米500元,設∠OMA=θ,記草坪栽植與新道路鋪設所需的總費用為f(θ).
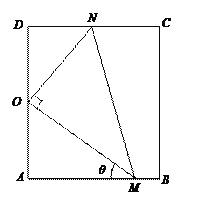
(1)求f(θ)關于θ函數關系式,并寫出定義域;
(2)為節約投入成本,當tanθ為何值時,總費用 f(θ)最小?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C對應的邊分別是a,b,c,已知cos2A﹣3cos(B+C)=1.
(Ⅰ)求角A的大小;
(Ⅱ)若△ABC的面積S=5 ![]() ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)是定義在R上的偶函數,且對任意的x∈R恒有f(x+1)=f(x-1),
已知當x∈[0,1]時f(x)=(![]() )1-x,則
)1-x,則
①2是函數f(x)的周期;
②函數f(x)在(1,2)上是減函數,在(2,3)上是增函數;
③函數f(x)的最大值是1,最小值是0;
④當x∈(3,4)時,f(x)=(![]() )x-3.
)x-3.
其中所有正確命題的序號是_______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線: ![]() ax+by=1(其中a,b是實數) 與圓:x2+y2=1(O是坐標原點)相交于A,B兩點,且△AOB是直角三角形,點P(a,b)是以點M(0,1)為圓心的圓M上的任意一點,則圓M的面積最小值為 .
ax+by=1(其中a,b是實數) 與圓:x2+y2=1(O是坐標原點)相交于A,B兩點,且△AOB是直角三角形,點P(a,b)是以點M(0,1)為圓心的圓M上的任意一點,則圓M的面積最小值為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知△ABC,|AB|=8,AC與BC邊所在直線的斜率之積為定值m,
(1)求動點C的軌跡方程;
(2)當m=1時,過點E(0,1)的直線l與曲線C相交于P、Q兩點,求P、Q兩點的中點M的軌跡方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com