
分析 先判斷a、c是正數,且ac=$\frac{1}{4}$,把所求的式子變形使用基本不等式求最小值.
解答 解:∵二次函數f(x)=ax2-x+c的值域為[0,+∞),
∴$\left\{\begin{array}{l}{a>0}\\{△=1-4ac=0}\end{array}\right.$,
解得a>0,c>0,ac=$\frac{1}{4}$.
∴$\frac{2}{a}$+$\frac{2}{c}$≥2$\sqrt{\frac{2}{a}•\frac{2}{c}}$=8,當且僅當a=c=$\frac{1}{2}$時取等號,
∴$\frac{2}{a}$+$\frac{2}{c}$的最小值為8,
故答案為:8
點評 本題考查函數的值域及基本不等式的應用,求解的關鍵就是拆項,屬于基礎題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
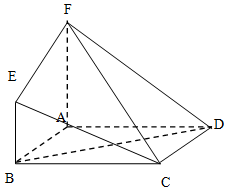 已知空間幾何體ABCDEF中,四邊形ABCD是正方形,AF⊥平面ABCD,BE⊥平面ABCD,AB=AF=2BE.
已知空間幾何體ABCDEF中,四邊形ABCD是正方形,AF⊥平面ABCD,BE⊥平面ABCD,AB=AF=2BE.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 在矩形ABCD中,以DA所在直線為x軸,以DA中點O為坐標原點,建立如圖所示的平面直角坐標系.已知點B的坐標為(3,2),E、F為AD的兩個三等分點,AC和BF交于點G,△BEG的外接圓為⊙H.
在矩形ABCD中,以DA所在直線為x軸,以DA中點O為坐標原點,建立如圖所示的平面直角坐標系.已知點B的坐標為(3,2),E、F為AD的兩個三等分點,AC和BF交于點G,△BEG的外接圓為⊙H.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 若sin A=sin B,則A=B | B. | 若lgx2=0,則x=1 | ||
| C. | ?x∈R,都有x2+1>0 | D. | ?x0∈Z,使1<4x0<3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com