
活動:教師引導學生探究,能否構造三角形,使EF作為三角形中位線,借助于三角形中位線定理解決,或創造相同起點,以建立向量間關系.鼓勵學生多角度觀察思考問題.

圖5
解:方法一:過點C在平面內作![]() =
=![]() ,
,
則四邊形ABGC是平行四邊形,
故F為AG中點.(如圖5)
∴EF是△ADG的中位線.
∴EF![]()
![]() DG
DG
∴![]() =
=![]()
![]() .
.
而![]() =
=![]() +
+![]() =
=![]() +
+![]() ,
,
∴![]() =
=![]() (
(![]() +
+![]() ).
).
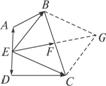
圖6
方法二:如圖6,連接EB、EC,則有![]() =
=![]() +
+![]() ,
,![]() =
=![]() +
+![]() ,
,
又∵E是AD的中點,
∴有![]() +
+![]() =0,
=0,
即有![]() +
+![]() =
=![]() +
+![]() .
.
以![]() 與
與![]() 為鄰邊作
為鄰邊作![]() EBGC,則由F是BC之中點,可得F也是EG之中點.
EBGC,則由F是BC之中點,可得F也是EG之中點.
∴![]() =
=![]()
![]() =
=![]() (
(![]() +
+![]() )=
)=![]() (
(![]() +
+![]() ).
).
點評:向量的運算主要從以下幾個方面加強練習:(1)加強數形結合思想的訓練,畫出草圖幫助解決問題;(2)加強三角形法則和平行四邊形法則的運用練習,做到準確熟練運用.


科目:高中數學 來源: 題型:
| 1 |
| A |
| 1 |
| B |
| 1 |
| C |
| 9 |
| π |
| 1 |
| A |
| 1 |
| B |
| 1 |
| C |
| 1 |
| D |
| 16 |
| 2π |
| 1 |
| A |
| 1 |
| B |
| 1 |
| C |
| 1 |
| D |
| 1 |
| E |
| 25 |
| 3π |
查看答案和解析>>
科目:高中數學 來源:2010-2011學年浙江省臺州市高三(上)期末數學試卷(文科)(解析版) 題型:填空題
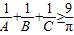 成立;在凸四邊形ABCD中,不等式
成立;在凸四邊形ABCD中,不等式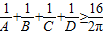 成立;在凸五邊形ABCDE中,不等式
成立;在凸五邊形ABCDE中,不等式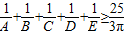 成立.根據以上情況,猜想在凸n邊形A1A2…An(n≥3)中的成立的不等式是 .
成立.根據以上情況,猜想在凸n邊形A1A2…An(n≥3)中的成立的不等式是 .查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com