
【題目】2018年12月1日,貴陽市地鐵一號線全線開通,在一定程度上緩解了出行的擁堵狀況.為了了解市民對地鐵一號線開通的關注情況,某調查機構在地鐵開通后的某兩天抽取了部分乘坐地鐵的市民作為樣本,分析其年齡和性別結構,并制作出如下等高條形圖:
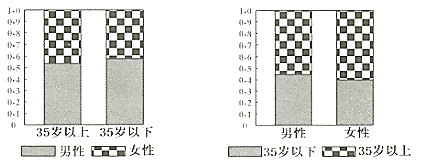
根據圖中(![]() 歲以上含
歲以上含![]() 歲)的信息,下列結論中不一定正確的是( )
歲)的信息,下列結論中不一定正確的是( )
A. 樣本中男性比女性更關注地鐵一號線全線開通
B. 樣本中多數女性是![]() 歲以上
歲以上
C. ![]() 歲以下的男性人數比
歲以下的男性人數比![]() 歲以上的女性人數多
歲以上的女性人數多
D. 樣本中![]() 歲以上的人對地鐵一號線的開通關注度更高
歲以上的人對地鐵一號線的開通關注度更高
 狀元坊全程突破導練測系列答案
狀元坊全程突破導練測系列答案科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐![]() 中,底面是邊長為4的正三角形,
中,底面是邊長為4的正三角形,![]() 底面
底面![]() ,點
,點![]() 分別為
分別為![]() 的中點,且異面直線
的中點,且異面直線![]() 和
和![]() 所成的角的大小為
所成的角的大小為![]() .
.
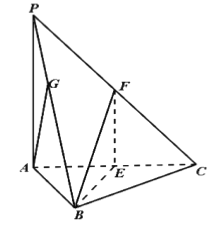
(1)求證:平面![]() 平面
平面![]() ;
;
(2)求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高校在![]() 年的自主招生考試成績中隨機抽取
年的自主招生考試成績中隨機抽取![]() 名學生的筆試成績,按成績分組:第
名學生的筆試成績,按成績分組:第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() 得到的頻率分布直方圖如圖所示
得到的頻率分布直方圖如圖所示
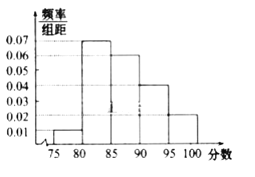
![]() 分別求第
分別求第![]() 組的頻率;
組的頻率;
![]() 若該校決定在第
若該校決定在第![]() 組中用分層抽樣的方法抽取
組中用分層抽樣的方法抽取![]() 名學生進入第二輪面試,
名學生進入第二輪面試,
![]() 已知學生甲和學生乙的成績均在第
已知學生甲和學生乙的成績均在第![]() 組,求學生甲和學生乙同時進入第二輪面試的概率;
組,求學生甲和學生乙同時進入第二輪面試的概率;
![]() 根據直方圖試估計這
根據直方圖試估計這![]() 名學生成績的平均分.(同一組中的數據用改組區間的中間值代表)
名學生成績的平均分.(同一組中的數據用改組區間的中間值代表)
查看答案和解析>>
科目:高中數學 來源: 題型:
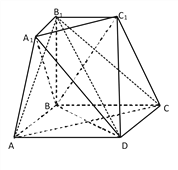
【題目】如圖所示的幾何體是由棱臺![]() 和棱錐
和棱錐![]() 拼接而成的組合體,其底面四邊形
拼接而成的組合體,其底面四邊形![]() 是邊長為
是邊長為![]() 的菱形,且
的菱形,且![]() ,
, ![]()
![]() 平面
平面![]() ,
, ![]() .
.
(1)求證:平面![]()
![]() 平面
平面![]()
![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四棱錐![]() 中,
中,![]() ,
,![]() .M為CD的中點.
.M為CD的中點.

(1)若點E為PC的中點,求證:BE∥平面PAD;
(2)當平面PBD⊥平面ABCD時,求點A到平面CEM的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知焦點在![]() 軸上的拋物線
軸上的拋物線![]() 過點
過點![]() ,橢圓
,橢圓![]() 的兩個焦點分別為
的兩個焦點分別為![]() ,
,![]() ,其中
,其中![]() 與
與![]() 的焦點重合,過點
的焦點重合,過點![]() 與
與![]() 的長軸垂直的直線交
的長軸垂直的直線交![]() 于
于![]() ,
,![]() 兩點,且
兩點,且![]() ,曲線
,曲線![]() 是以坐標原點
是以坐標原點![]() 為圓心,以
為圓心,以![]() 為半徑的圓.
為半徑的圓.
(1)求![]() 與
與![]() 的標準方程;
的標準方程;
(2)若動直線![]() 與
與![]() 相切,且與
相切,且與![]() 交于
交于![]() ,
,![]() 兩點,求
兩點,求![]() 的面積
的面積![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某企業生產的某種產品中抽取100件,測量這些產品的一項質量指標值,由測量表得如下頻數分布表:
質量指標值分組 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
頻數 | 6 | 26 | 38 | 22 | 8 |
(I)在答題卡上作出這些數據的頻率分布直方圖:

(II)估計這種產品質量指標值的平均數及方差(同一組中的數據用該組區間的中點值作代表);
(III)根據以上抽樣調查數據,能否認為該企業生產的這種產品符合“質量指標值不低于95的產品至少要占全部產品的80%”的規定?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com