
| 已知:y=f(x)定義域為[-1,1],且滿足:f(-1)=f(1)=0,對任意u,v∈[-1,1],都有|f(u)-f(v)|≤|u-v|, (1)判斷函數p(x)=x2-1是否滿足題設條件? (2)判斷函數g(x)=  ,是否滿足題設條件? ,是否滿足題設條件? |
| 解:(1)若u,v∈[-1,1],|p(u)-p(v)|=|u2-v2|=|(u+v)(u-v)|, 取u= 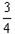 ∈[-1,1],v= ∈[-1,1],v=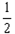 ∈[-1,1], ∈[-1,1],則|p(u)-p(v)|=|(u+v)(u-v)|=  |u-v|>|u-v|, |u-v|>|u-v|,所以p(x)不滿足題設條件。 (2)分三種情況討論: 10.若u,v∈[-1,0],則|g(u)-g(v)|=|(1+u)-(1+v)|=|u-v|,滿足題設條件; 20.若u,v∈[0,1],則|g(u)-g(v)|=|(1-u)-(1-v)|=|v-u|,滿足題設條件; 30.若u∈[-1,0],v∈[0,1], 則:|g(u)-g(v)|=|(1-u)-(1+v)|=|-u-v|=|v+u|≤|v-u|=|u-v|,滿足題設條件; 40.若u∈[0,1],v∈[-1,0],同理可證滿足題設條件; 綜合上述得g(x)滿足條件。 |


科目:高中數學 來源: 題型:
 已知冪函數y=f(x)的圖象經過點(2,4),對于偶函數y=g(x)(x∈R),當x≥0時,g(x)=f(x)-2x.
已知冪函數y=f(x)的圖象經過點(2,4),對于偶函數y=g(x)(x∈R),當x≥0時,g(x)=f(x)-2x.查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,已知:射線OA為y=kx(k>0,x>0),射線OB為y=-kx(x>0),動點P(x,y)在∠AOx的內部,PM⊥OA于M,PN⊥OB于N,四邊形ONPM的面積恰為k.
如圖,已知:射線OA為y=kx(k>0,x>0),射線OB為y=-kx(x>0),動點P(x,y)在∠AOx的內部,PM⊥OA于M,PN⊥OB于N,四邊形ONPM的面積恰為k.查看答案和解析>>
科目:高中數學 來源: 題型:
| a•2x | ||
2x+
|
| 2 |
| OP |
| 1 |
| 2 |
| OP1 |
| OP2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com