
【題目】已知數列{an}滿足a1=81,an= ![]() (k∈N*),則數列{an}的前n項和Sn的最大值為
(k∈N*),則數列{an}的前n項和Sn的最大值為
【答案】127
【解析】解:∵數列{an}滿足a1=81,an= ![]() (k∈N*),∴n=2k(k∈N*)時,a2k=﹣1+log3a2k﹣1 , a2=3;n=2k+1時a2k+1=
(k∈N*),∴n=2k(k∈N*)時,a2k=﹣1+log3a2k﹣1 , a2=3;n=2k+1時a2k+1= ![]() .
.
∴a2k+1= ![]() =
= ![]() ,a2k=﹣1+a2k﹣2 .
,a2k=﹣1+a2k﹣2 .
∴數列{an}的奇數項成等比數列,公比為 ![]() ;偶數項成等差數列,公差為﹣1.
;偶數項成等差數列,公差為﹣1.
∴Sn=S2k=(a1+a3+…+a2k﹣1)+(a2+a4+…+a2k)
= 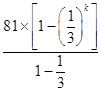 +3k+
+3k+ ![]()
= 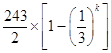 ﹣
﹣ ![]() +
+ ![]() ≤127.(k=5時取等號).
≤127.(k=5時取等號).
Sn=S2k﹣1=S2k﹣2+a2k﹣1= 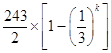 ﹣
﹣ ![]() +
+ ![]() +
+ ![]() ≤111,k=5時取等號.
≤111,k=5時取等號.
綜上可得:數列{an}的前n項和Sn的最大值為127.
所以答案是:127.


科目:高中數學 來源: 題型:
【題目】設函數f(x)=aexlnx+ ![]() ,曲線y=f(x)在點(1,f(1))處得切線方程為y=e(x﹣1)+2.
,曲線y=f(x)在點(1,f(1))處得切線方程為y=e(x﹣1)+2.
(Ⅰ)求a、b;
(Ⅱ)證明:f(x)>1.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合M={x|9x﹣43x+1+27=0},N={x|log2(x+1)+log2x=log26},則M、N的關系是( )
A.MN
B.NM
C.M=N
D.不確定
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法正確的是( ).
A. ![]() ,“
,“![]() ”是“
”是“![]() ”的必要不充分條件
”的必要不充分條件
B. “![]() 且
且![]() 為真命題”是“
為真命題”是“![]() 或
或![]() 為真命題” 的必要不充分條件
為真命題” 的必要不充分條件
C. 命題“![]() ,使得
,使得![]() ”的否定是:“
”的否定是:“![]() ”
”
D. 命題![]() :“
:“![]() ”,則
”,則![]() 是真命題
是真命題
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校100名學生期中考試數學成績的頻率分布直方圖如圖所示,其中成績分組區間如下:
組號 | 第一組 | 第二組 | 第三組 | 第四組 | 第五組 |
分組 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |

(1)求圖中a的值;
(2)根據頻率分布直方圖,估計這100名學生期中考試數學成績的平均分;
(3)現用分層抽樣的方法從第3、4、5組中隨機抽取6名學生,將該樣本看成一個總體,從中隨機抽取2名,求其中恰有1人的分數不低于90分的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在數列{ ![]() }中,已知
}中,已知![]() ,
,![]() ,
,![]() ,則
,則![]() 等于( )
等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
將數列的等式關系兩邊取倒數![]() 是公差為
是公差為![]() 的等差數列,再根據等差數列求和公式得到數列通項
的等差數列,再根據等差數列求和公式得到數列通項![]() ,再取倒數即可得到數列{
,再取倒數即可得到數列{![]() }的通項.
}的通項.
將等式![]() 兩邊取倒數得到
兩邊取倒數得到![]() ,
,![]() 是公差為
是公差為![]() 的等差數列,
的等差數列,![]() =
=![]() ,根據等差數列的通項公式的求法得到
,根據等差數列的通項公式的求法得到![]() ,故
,故![]() =
=![]() .
.
故答案為:B.
【點睛】
這個題目考查的是數列通項公式的求法,數列通項的求法中有常見的已知![]() 和
和![]() 的關系,求
的關系,求![]() 表達式,一般是寫出
表達式,一般是寫出![]() 做差得通項,但是這種方法需要檢驗n=1時通項公式是否適用;還有構造新數列的方法,取倒數,取對數的方法等等.
做差得通項,但是這種方法需要檢驗n=1時通項公式是否適用;還有構造新數列的方法,取倒數,取對數的方法等等.
【題型】單選題
【結束】
9
【題目】在如圖所示的銳角三角形空地中, 欲建一個面積不小于300m2的內接矩形花園(陰影部分), 則其邊長x(單位m)的取值范圍是 ( )

(A) [15,20](B) [12,25] (C) [10,30](D) [20,30]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 是遞增數列,且對
是遞增數列,且對![]() ,都有
,都有![]() ,則實數
,則實數![]() 的取值范圍是
的取值范圍是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
由{an}是遞增數列,得到an+1>an,再由“an=n2+λn恒成立”轉化為“λ>﹣2n﹣1對于n∈N*恒成立”求解.
∵{an}是遞增數列,
∴an+1>an,
∵an=n2+λn恒成立
即(n+1)2+λ(n+1)>n2+λn,
∴λ>﹣2n﹣1對于n∈N*恒成立.
而﹣2n﹣1在n=1時取得最大值﹣3,
∴λ>﹣3,
故選:D.
【點睛】
本題主要考查由數列的單調性來構造不等式,解決恒成立問題.研究數列單調性的方法有:比較相鄰兩項間的關系,將an+1和an做差與0比較,即可得到數列的單調性;研究數列通項即數列表達式的單調性.
【題型】單選題
【結束】
13
【題目】已知數列{an}滿足a1=1,且an=an-1+2n![]() 1 (n≥2 ),則a20=________.
1 (n≥2 ),則a20=________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】等差數列{an}的各項均為正數,a1=3,前n項和為Sn,{bn}為等比數列,b1=1,且b2S2=64,b3S3=960.
(1)求an與bn;
(2)求![]()
【答案】(1)an=2n+1,bn=8n-1.(2)![]()
【解析】
(1)設{an}的公差為d,{bn}的公比為q,由題設條件建立方程組,解方程組得到d和q的值,從而求出an與bn;(2)由Sn=n(n+2),知![]() ,由此可求出
,由此可求出![]() 的值.
的值.
(1)設{an}的公差為d,{bn}的公比為q,則d為正數,
an=3+(n-1)d,bn=qn-1,
依題意有![]() ,
,
解得![]() 或
或 (舍去).
(舍去).
故an=3+2(n-1)=2n+1,bn=8n-1.
(2)Sn=3+5+…+(2n+1)=n(n+2).
所以![]() +
+![]() +…+
+…+![]() =
=![]() +
+![]() +
+![]() +…+
+…+![]()
=![]() (1-
(1-![]() +
+![]() -
-![]() +
+![]() -
-![]() +…+
+…+![]() -
-![]() )
)
=![]() (1+
(1+![]() -
-![]() -
-![]() )
)
=![]() -
-![]() .
.
【點睛】
這個題目考查的是數列通項公式的求法及數列求和的常用方法;數列通項的求法中有常見的已知![]() 和
和![]() 的關系,求
的關系,求![]() 表達式,一般是寫出
表達式,一般是寫出![]() 做差得通項,但是這種方法需要檢驗n=1時通項公式是否適用;數列求和常用法有:錯位相減,裂項求和,分組求和等。
做差得通項,但是這種方法需要檢驗n=1時通項公式是否適用;數列求和常用法有:錯位相減,裂項求和,分組求和等。
【題型】解答題
【結束】
21
【題目】已知函數f(x)滿足f(x+y)=f(x)·f(y),且f(1)=![]() .
.
(1)當n∈N+,求f(n)的表達式;
(2)設an=nf(n),n∈N+,求證:a1+a2+…+an<2.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國是世界上嚴重缺水的國家,某市政府為了鼓勵居民節約用水,計劃調整居民生活用水收費方案,擬確定一個合理的月用水量標準![]() (噸)、一位居民的月用水量不超過
(噸)、一位居民的月用水量不超過![]() 的部分按平價收費,超出
的部分按平價收費,超出![]() 的部分按議價收費.為了了解居民用水情況,通過抽樣,獲得了某年100位居民每人的月均用水量(單位:噸),將數據按照[0,0.5),[0.5,1),…,[4,4.5]分成9組,制成了如圖所示的頻率分布直方圖.
的部分按議價收費.為了了解居民用水情況,通過抽樣,獲得了某年100位居民每人的月均用水量(單位:噸),將數據按照[0,0.5),[0.5,1),…,[4,4.5]分成9組,制成了如圖所示的頻率分布直方圖.

(Ⅰ)求直方圖中a的值;
(Ⅱ)設該市有30萬居民,估計全市居民中月均用水量不低于3噸的人數,并說明理由;
(Ⅲ)若該市政府希望使85%的居民每月的用水量不超過標準![]() (噸),估計
(噸),估計![]() 的值,并說明理由.
的值,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com