
【題目】某鮮奶店每天購進30瓶鮮牛奶,且當天的利潤y(單位:元)關于當天需求量n(單位:瓶,n∈N)的函數解析式![]() (n∈N).鮮奶店記錄了100天鮮牛奶的日需求量(單位:瓶)繪制出如下的柱形圖(例如:日需求量為25瓶時,頻數為5):
(n∈N).鮮奶店記錄了100天鮮牛奶的日需求量(單位:瓶)繪制出如下的柱形圖(例如:日需求量為25瓶時,頻數為5):
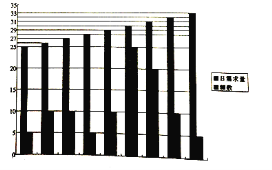
(1)求這100天的日利潤(單位:元)的平均數;
(2)以100天記錄的各需求量的頻率作為各需求量發生的概率,求當天的利潤不少于100元的概率.
 期末好成績系列答案
期末好成績系列答案 99加1領先期末特訓卷系列答案
99加1領先期末特訓卷系列答案 百強名校期末沖刺100分系列答案
百強名校期末沖刺100分系列答案 好成績1加1期末沖刺100分系列答案
好成績1加1期末沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】某種汽車的購車費用是10萬元,每年使用的保險費、養路費、汽油費約為![]() 萬元,年維修費用第一年是
萬元,年維修費用第一年是![]() 萬元,第二年是
萬元,第二年是![]() 萬元,第三年是
萬元,第三年是![]() 萬元,…,以后逐年遞增
萬元,…,以后逐年遞增![]() 萬元汽車的購車費用、每年使用的保險費、養路費、汽油費、維修費用的和平均攤到每一年的費用叫做年平均費用.設這種汽車使用
萬元汽車的購車費用、每年使用的保險費、養路費、汽油費、維修費用的和平均攤到每一年的費用叫做年平均費用.設這種汽車使用![]() 年的維修費用的和為
年的維修費用的和為![]() ,年平均費用為
,年平均費用為![]() .
.
(1)求出函數![]() ,
,![]() 的解析式;
的解析式;
(2)這種汽車使用多少年時,它的年平均費用最小?最小值是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (t為參數),直線
(t為參數),直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數).設
為參數).設![]() 與
與![]() 的交點為
的交點為![]() ,當
,當![]() 變化時,
變化時,![]() 的軌跡為曲線
的軌跡為曲線![]()
(1)寫出![]() 的普通方程;
的普通方程;
(2)以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系,設
軸正半軸為極軸建立極坐標系,設![]() ,
,![]() 為
為![]() 與
與![]() 的交點,求
的交點,求![]() 的極徑.
的極徑.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年上半年我國多個省市暴發了“非洲豬瘟”疫情,生豬大量病死,存欄量急劇下降,一時間豬肉價格暴漲,其他肉類價格也跟著大幅上揚,嚴重影響了居民的生活.為了解決這個問題,我國政府一方面鼓勵有條件的企業和散戶防控疫情,擴大生產;另一方面積極向多個國家開放豬肉進口,擴大肉源,確保市場供給穩定.某大型生豬生產企業分析當前市場形勢,決定響應政府號召,擴大生產,決策層調閱了該企業過去生產相關數據,就“一天中一頭豬的平均成本與生豬存欄數量之間的關系”進行研究.現相關數據統計如下表:
生豬存欄數量 | 2 | 3 | 4 | 5 | 8 |
頭豬每天平均成本 | 3.2 | 2.4 | 2 | 1.9 | 1.5 |
(1)研究員甲根據以上數據認為![]() 與
與![]() 具有線性回歸關系,請幫他求出
具有線性回歸關系,請幫他求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() (保留小數點后兩位有效數字)
(保留小數點后兩位有效數字)
(2)研究員乙根據以上數據得出![]() 與
與![]() 的回歸模型:
的回歸模型:![]() .為了評價兩種模型的擬合結果,請完成以下任務:
.為了評價兩種模型的擬合結果,請完成以下任務:
①完成下表(計算結果精確到0.01元)(備注:![]() 稱為相應于點
稱為相應于點![]() 的殘差);
的殘差);
生豬存欄數量 | 2 | 3 | 4 | 5 | 8 | |
頭豬每天平均成本 | 3.2 | 2.4 | 2 | 1.9 | 1.5 | |
模型甲 | 估計值 | |||||
殘差 | ||||||
模型乙 | 估計值 | 3.2 | 2.4 | 2 | 1.76 | 1.4 |
殘差 | 0 | 0 | 0 | 0.14 | 0.1 | |
②分別計算模型甲與模型乙的殘差平方和![]() 及
及![]() ,并通過比較
,并通過比較![]() 與
與![]() 的大小,判斷哪個模型擬合效果更好;
的大小,判斷哪個模型擬合效果更好;
(3)根據市場調查,生豬存欄數量達到1萬頭時,飼養一頭豬每一天的平均收入為7.5元;生豬存欄數量達到1.2萬頭時,飼養一頭豬每一天的平均收入為7.2元.若按(2)中擬合效果較好的模型計算一天中一頭豬的平均成本,問該生豬存欄數量選擇1萬頭還是1.2萬頭能獲得更多利潤?請說明理由.(利潤=收入-成本)
參考公式: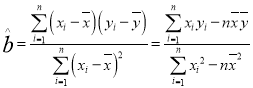 ,
,![]()
參考數據: ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設拋物線![]() 的焦點為
的焦點為![]() ,過點
,過點![]() 的直線與拋物線相交于
的直線與拋物線相交于![]() 兩點,與拋物線的準線相交于點
兩點,與拋物線的準線相交于點![]() ,
, ![]() ,則
,則![]() 與
與![]() 的面積之比
的面積之比![]() __________.
__________.
【答案】![]()
【解析】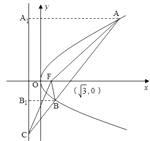
由題意可得拋物線的焦點![]() 的坐標為
的坐標為![]() ,準線方程為
,準線方程為![]() 。
。
如圖,設![]() ,過A,B分別向拋物線的準線作垂線,垂足分別為E,N,則
,過A,B分別向拋物線的準線作垂線,垂足分別為E,N,則
![]() ,解得
,解得![]() 。
。
把![]() 代入拋物線
代入拋物線![]() ,解得
,解得![]() 。
。
∴直線AB經過點![]() 與點
與點![]() ,
,
故直線AB的方程為![]() ,代入拋物線方程解得
,代入拋物線方程解得![]() 。
。
∴![]() 。
。
在![]() 中,
中, ![]() ,
,
∴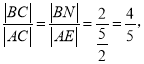
∴![]() 。答案:
。答案: ![]()
點睛:
在解決與拋物線有關的問題時,要注意拋物線的定義在解題中的應用。拋物線定義有兩種用途:一是當已知曲線是拋物線時,拋物線上的點M滿足定義,它到準線的距離為d,則|MF|=d,可解決有關距離、最值、弦長等問題;二是利用動點滿足的幾何條件符合拋物線的定義,從而得到動點的軌跡是拋物線.
【題型】填空題
【結束】
17
【題目】已知![]() 三個內角
三個內角![]() 所對的邊分別是
所對的邊分別是![]() ,若
,若![]() .
.
(1)求角![]() ;
;
(2)若![]() 的外接圓半徑為2,求
的外接圓半徑為2,求![]() 周長的最大值.
周長的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】學校藝術節對同一類的![]() ,
,![]() ,
,![]() ,
,![]() 四項參賽作品,只評一項一等獎,在評獎揭曉前,甲、乙、丙、丁四位同學對這四項參賽作品預測如下:
四項參賽作品,只評一項一等獎,在評獎揭曉前,甲、乙、丙、丁四位同學對這四項參賽作品預測如下:
甲說:“是![]() 或
或![]() 作品獲得一等獎”;
作品獲得一等獎”;
乙說:“![]() 作品獲得一等獎”;
作品獲得一等獎”;
丙說:“![]() ,
,![]() 兩項作品未獲得一等獎”;
兩項作品未獲得一等獎”;
丁說:“是![]() 作品獲得一等獎”.
作品獲得一等獎”.
若這四位同學中只有兩位說的話是對的,則獲得一等獎的作品是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對某產品1到6月份銷售量及其價格進行調查,其售價x和銷售量y之間的一組數據如下表所示:
月份i | 1 | 2 | 3 | 4 | 5 | 6 |
單價 | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
銷售量 | 11 | 10 | 8 | 6 | 5 | 14 |
(1)根據1至5月份的數據,求出y關于x的回歸直線方程;
(2)若由回歸直線方程得到的估計數據與剩下的檢驗數據的誤差不超過0.5元,則認為所得到的回歸直線方程是理想的,試問所得到的回歸直線方程是否理想?
(3)預計在今后的銷售中,銷售量與單價仍然服從(1)中的關系,且該產品的成本是2.5元/件,為獲得最大利潤,該產品的單價應定為多少元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】學校書店新進了一套精品古典四大名著:《紅樓夢》、《三國演義》、《西游記》、《水滸傳》共四本書,每本名著數量足夠多,今有五名同學去書店買書,由于價格較高,五名同學打算每人只選擇一本購買.
(1)求“每本書都有同學買到”的概率;
(2)求“對于每個同學,均存在另一個同學與其購買的書相同”的概率;
(3)記X為五位同學購買相同書的個數的最大值,求X的分布列和數學期望E(X).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com