
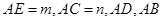 為方程
為方程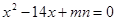 的兩根,
的兩根,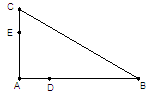
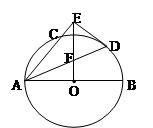
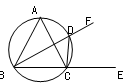
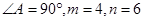 ,求C,B,D,E四點所在圓的半徑。
,求C,B,D,E四點所在圓的半徑。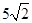
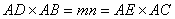
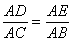 .又∠DAE=∠CAB,從而△ADE∽△ACB 因此∠ADE=∠ACB , 所以C,B,D,E四點共圓。
.又∠DAE=∠CAB,從而△ADE∽△ACB 因此∠ADE=∠ACB , 所以C,B,D,E四點共圓。 (12-2)=5.
(12-2)=5.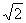


科目:高中數學 來源:不詳 題型:解答題
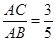 ,求
,求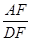 的值.
的值.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
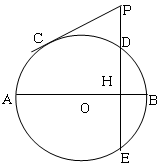
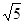 ,求PD的長.
,求PD的長.查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
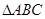 ,過頂點A的圓與邊BC切于BC的中點P,與邊AB、AC分別交于點M、N,且CN=2BM,點N平分AC.則
,過頂點A的圓與邊BC切于BC的中點P,與邊AB、AC分別交于點M、N,且CN=2BM,點N平分AC.則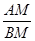 =( )
=( )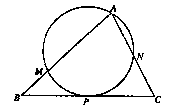
查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com