
【題目】已知橢圓![]() :
:![]() 過點
過點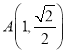 ,且以
,且以![]() ,
,![]()
![]() 為焦點,橢圓
為焦點,橢圓![]() 的離心率為
的離心率為![]() .
.
(1)求實數![]() 的值;
的值;
(2)過左焦點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 、
、![]() 兩點,
兩點,![]() 為坐標原點,問橢圓
為坐標原點,問橢圓![]() 上是否存在點
上是否存在點![]() ,使線段
,使線段![]() 和線段
和線段![]() 相互平分?若存在,求出點
相互平分?若存在,求出點![]() 的坐標,若不存在,說明理由。
的坐標,若不存在,說明理由。
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】在如圖所示的幾何體中,![]() 是邊長為2的正三角形,
是邊長為2的正三角形,![]() 平面ABC,平面
平面ABC,平面![]() 平面ABC,
平面ABC,![]() ,且
,且![]() .
.
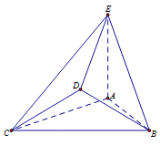
(1)若![]() ,求證:
,求證:![]() 平面BDE;
平面BDE;
(2)若二面角![]() 為
為![]() ,求直線CD與平面BDE所成角.
,求直線CD與平面BDE所成角.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,且點
,且點![]() 在橢圓
在橢圓![]() 上.
上.
(1)求橢圓![]() 的方程;
的方程;
(2)若橢圓![]() 的焦點在
的焦點在![]() 軸上,點
軸上,點![]() 為坐標原點,射線
為坐標原點,射線![]() 、
、![]() 分別與橢圓
分別與橢圓![]() 交于點
交于點![]() 、點
、點![]() ,且
,且![]() ,試判斷直線
,試判斷直線![]() 與圓
與圓![]() :
:![]() 的位置關系,并證明你的結論.
的位置關系,并證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給定數列![]() ,若數列
,若數列![]() 中任意(不同)兩項之和仍是該數列中的一項,則稱該數列是“封閉數列”.
中任意(不同)兩項之和仍是該數列中的一項,則稱該數列是“封閉數列”.
(1)已知數列![]() 的通項公式為
的通項公式為![]() ,試判斷
,試判斷![]() 是否為封閉數列,并說明理由;
是否為封閉數列,并說明理由;
(2)已知數列![]() 滿足
滿足![]() 且
且![]() ,設
,設![]() 是該數列
是該數列![]() 的前
的前![]() 項和,試問:是否存在這樣的“封閉數列”
項和,試問:是否存在這樣的“封閉數列”![]() ,使得對任意
,使得對任意![]() 都有
都有![]() ,且
,且![]() ,若存在,求數列
,若存在,求數列![]() 的首項
的首項![]() 的所有取值;若不存在,說明理由;
的所有取值;若不存在,說明理由;
(3)證明等差數列![]() 成為“封閉數列”的充要條件是:存在整數
成為“封閉數列”的充要條件是:存在整數![]() ,使
,使![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,《宋人撲棗圖軸》是作于宋朝的中國古畫,現收藏于中國臺北故宮博物院.該作品簡介:院角的棗樹結實累累,小孩群來攀扯,枝椏不停晃動,粒粒棗子搖落滿地,有的牽起衣角,有的捧著盤子拾取,又玩又吃,一片興高采烈之情,躍然于絹素之上.甲、乙、丙、丁四人想根據該圖編排一個舞蹈,舞蹈中他們要模仿該圖中小孩撲棗的爬、扶、撿、頂四個動作,四人每人模仿一個動作.若他們采用抽簽的方式來決定誰模仿哪個動作,則甲不模仿“爬”且乙不模仿“扶”的概率是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,已知橢圓![]() 的離心率為
的離心率為![]() ,右焦點到直線
,右焦點到直線![]() 的距離為1.
的距離為1.
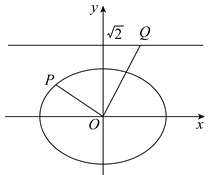
![]() 求橢圓的標準方程;
求橢圓的標準方程;
![]() 若P為橢圓上的一點
若P為橢圓上的一點![]() 點P不在y軸上
點P不在y軸上![]() ,過點O作OP的垂線交直線
,過點O作OP的垂線交直線![]() 于點Q,求
于點Q,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com