
【題目】某城市隨機抽取一年(365天)內100天的空氣質量指數![]() 的檢測數據,結果統計如下:
的檢測數據,結果統計如下:
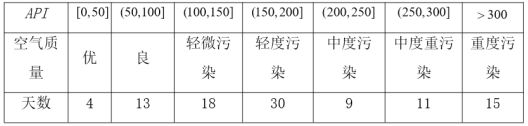
記某企業每天由空氣污染造成的經濟損失![]() (單位:元),空氣質量指數
(單位:元),空氣質量指數![]() 為
為![]() .在區間
.在區間![]() 對企業沒有造成經濟損失;在區間
對企業沒有造成經濟損失;在區間![]() 對企業造成經濟損失成直線模型(當
對企業造成經濟損失成直線模型(當![]() 為150時造成的經濟損失為500元,當
為150時造成的經濟損失為500元,當![]() 為200時,造成的經濟損失為700元);當
為200時,造成的經濟損失為700元);當![]() 大于300時造成的經濟損失為2000元.
大于300時造成的經濟損失為2000元.
(1)試寫出![]() 的表達式;
的表達式;
(2)試估計在本年內隨機抽取一天,該天經濟損失![]() 大于200元且不超過600元的概率;
大于200元且不超過600元的概率;
(3)若本次抽取的樣本數據有30天是在供暖季,其中有8天為重度污染,完成下面![]() 列聯表,并判斷
列聯表,并判斷
能否有![]() 的把握認為該市本年空氣重度污染與供暖有關?
的把握認為該市本年空氣重度污染與供暖有關?
附:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.32 | 2.07 | 2.70 | 3.74 | 5.02 | 6.63 | 7.87 | 10.82 |
![]()
非重度污染 | 重度污染 | 合計 | |
供暖季 | |||
非供暖季 | |||
合計 | 100 |
【答案】(1) 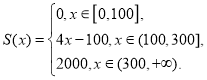 ;(2)
;(2) ![]() ;(3)列聯表見解析,有
;(3)列聯表見解析,有![]() 的把握認為該市本年空氣重度污染與供暖有關.
的把握認為該市本年空氣重度污染與供暖有關.
【解析】
試題分析:(1)根據在區間![]() 對企業沒有造成經濟損失;在區間
對企業沒有造成經濟損失;在區間![]() 對企業造成經濟損失成直線模型(當
對企業造成經濟損失成直線模型(當![]() 為
為![]() 時造成的經濟損失為
時造成的經濟損失為![]() 元,當
元,當![]() 為
為![]() 時,造成的經濟損失為
時,造成的經濟損失為![]() 元);當
元);當![]() 大于
大于![]() 時造成的經濟損失為
時造成的經濟損失為![]() 元,可得函數解析式;(2)由
元,可得函數解析式;(2)由![]() ,得
,得![]() ,頻數為
,頻數為![]() ,即可求出概率;(3)根據所給的數據,列出列聯表,根據所給的觀測值的公式,代入數據做出觀測值,同臨界值進行比較,即可得出結論.
,即可求出概率;(3)根據所給的數據,列出列聯表,根據所給的觀測值的公式,代入數據做出觀測值,同臨界值進行比較,即可得出結論.
試題解析:(1)根據在區間![]() 對企業沒有造成經濟損失;在區間
對企業沒有造成經濟損失;在區間![]() 對企業造成經濟損失成直線模型(當
對企業造成經濟損失成直線模型(當![]() 為
為![]() 時造成的經濟損失為
時造成的經濟損失為![]() 元,當
元,當![]() 為
為![]() 時,造成的經濟損失為
時,造成的經濟損失為![]() 元);當
元);當![]() 大于
大于![]() 時造成的經濟損失為
時造成的經濟損失為![]() 元,可得:
元,可得:
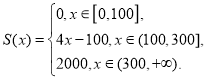
(2)設“在本年內隨機抽取一天,該天經濟損失![]() 大于
大于![]() 元且不超過
元且不超過![]() 元”為事件
元”為事件![]() ,
,
由![]() ,得
,得![]() ,頻數為39,
,頻數為39,![]() .
.
(3)根據以上數據得到如下列聯表:
非重度污染 | 重度污染 | 合計 | |
供暖季 |
|
|
|
非供暖季 |
|
|
|
合計 |
|
|
|
![]() 的觀測值
的觀測值![]() ,
,
所以有![]() 的把握認為空氣重度污染與供暖有關.
的把握認為空氣重度污染與供暖有關.


 勵耘書業暑假銜接寧波出版社系列答案
勵耘書業暑假銜接寧波出版社系列答案科目:高中數學 來源: 題型:
【題目】某校高一(1)班的一次數學測試成績的莖葉圖和頻率分布直方圖都受到不同程度的污損,可見部分如圖.
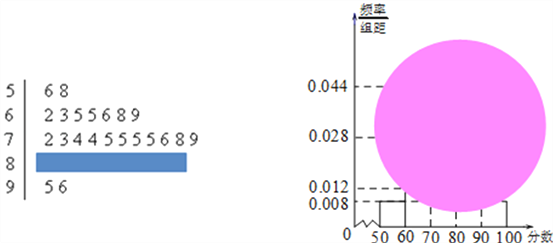
(Ⅰ)求分數在[50,60)的頻率及全班人數;
(Ⅱ)求分數在[80,90)之間的頻數,并計算頻率分布直方圖中[80,90)間矩形的高;
(Ⅲ)若要從分數在[80,100)之間的試卷中任取兩份分析學生失分情況,求在抽取的試卷中,至少有一份分數在[90,100)之間的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種商品原來每件售價為25元,年銷售8萬件.
(1)據市場調查,若價格每提高1元,銷售量將相應減少2000件,要使銷售的總收入不低于原收入,該商品每件定價最多為多少元?
(2)為了擴大該商品的影響力,提高年銷售量,公司決定明年對該商品進行全面技術革新和營銷策略改革,并提高定價到![]() 元,公司擬投入
元,公司擬投入![]() 萬元作為技改費用,投入50萬元作為固定宣傳費用,投入
萬元作為技改費用,投入50萬元作為固定宣傳費用,投入![]() 作為浮動宣傳費用.試問:當該商品明年的銷售量
作為浮動宣傳費用.試問:當該商品明年的銷售量![]() 至少應達到多少萬件時,才可能使明年的銷售收入不低于原收入與總投入之和?并求出此時商品的每件定價.
至少應達到多少萬件時,才可能使明年的銷售收入不低于原收入與總投入之和?并求出此時商品的每件定價.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系中,以坐標原點為極點,![]() 軸為正半軸建立極坐標系,圓
軸為正半軸建立極坐標系,圓![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 的參數方程為
的參數方程為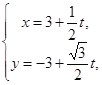 (t為參數).
(t為參數).
(1)求圓![]() 的直角坐標方程;
的直角坐標方程;
(2)求直線![]() 分圓
分圓![]() 所得的兩弧程度之比.
所得的兩弧程度之比.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】袋中有20個大小相同的球,其中記上0號的有10個,記上n號的有n個(n=1,2,3,4),現從袋中任取一球,X表示所取球的標號.
(1)求X的分布列,均值和方差;
(2)若Y=aX+b,E(Y)=1,D(Y)=11,試求a,b的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com