
【題目】雙曲線x2﹣ ![]() =1(b>0)的左、右焦點分別為F1 , F2 , 直線l過F2且與雙曲線交于A,B兩點.
=1(b>0)的左、右焦點分別為F1 , F2 , 直線l過F2且與雙曲線交于A,B兩點.
(1)直線l的傾斜角為 ![]() ,△F1AB是等邊三角形,求雙曲線的漸近線方程;
,△F1AB是等邊三角形,求雙曲線的漸近線方程;
(2)設b= ![]() ,若l的斜率存在,且(
,若l的斜率存在,且( ![]() +
+ ![]() )
) ![]() =0,求l的斜率.
=0,求l的斜率.
【答案】
(1)解:雙曲線x2﹣ ![]() =1(b>0)的左、右焦點分別為F1,F2,a=1,c2=1+b2,
=1(b>0)的左、右焦點分別為F1,F2,a=1,c2=1+b2,
直線l過F2且與雙曲線交于A,B兩點,
直線l的傾斜角為 ![]() ,△F1AB是等邊三角形,
,△F1AB是等邊三角形,
可得:A(c,b2),可得: ![]() ,
,
3b4=4(a2+b2),
即3b4﹣4b2﹣4=0,
b>0,解得b2=2.
所求雙曲線方程為:x2﹣ ![]() =1,
=1,
其漸近線方程為y=± ![]() x
x
(2)解:b= ![]() ,雙曲線x2﹣
,雙曲線x2﹣ ![]() =1,可得F1(﹣2,0),F2(2,0).
=1,可得F1(﹣2,0),F2(2,0).
設A(x1,y1),B(x2,y2),直線的斜率為:k= ![]() ,
,
直線l的方程為:y=k(x﹣2),
由題意可得: 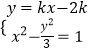 ,消去y可得:(3﹣k2)x2+4k2x﹣4k2﹣3=0,
,消去y可得:(3﹣k2)x2+4k2x﹣4k2﹣3=0,
△=36(1+k2)>0,
可得x1+x2= ![]() ,
,
則y1+y2=k(x1+x2﹣4)=k( ![]() ﹣4)=
﹣4)= ![]() .
.
![]() =(x1+2,y1),
=(x1+2,y1),
![]() =(x2+2,y2),
=(x2+2,y2),
( ![]() +
+ ![]() )
) ![]() =0可得:(x1+x2+4,y1+y2)(x1﹣x2,y1﹣y2)=0,
=0可得:(x1+x2+4,y1+y2)(x1﹣x2,y1﹣y2)=0,
可得x1+x2+4+(y1+y2)k=0,
得 ![]() +4+
+4+ ![]() k=0
k=0
可得:k2= ![]() ,
,
解得k=± img src="http://thumb.zyjl.cn/questionBank/Upload/2017/02/11/05/40d23035/SYS201702110503548573774059_DA/SYS201702110503548573774059_DA.016.png" width="22" height="34" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" /> .
l的斜率為:± ![]()
【解析】(1)利用直線的傾斜角,求出AB,利用三角形是正三角形,求解b,即可得到雙曲線方程.(2)求出左焦點的坐標,設出直線方程,推出A、B坐標,利用向量的數量積為0,即可求值直線的斜率.


 中考解讀考點精練系列答案
中考解讀考點精練系列答案科目:高中數學 來源: 題型:
【題目】設a<1,集合A={x∈R|x>0},B={x∈R|2x2﹣3(1+a)x+6a>0},D=A∩B.
(1)求集合D(用區間表示);
(2)求函數f(x)=2x3﹣3(1+a)x2+6ax在D內的極值點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工藝品廠要設計一個如圖1所示的工藝品,現有某種型號的長方形材料如圖2所示,其周長為4m,這種材料沿其對角線折疊后就出現圖1的情況.如圖,ABCD(AB>AD)為長方形的材料,沿AC折疊后AB'交DC于點P,設△ADP的面積為S2 , 折疊后重合部分△ACP的面積為S1 .
(Ⅰ)設AB=xm,用x表示圖中DP的長度,并寫出x的取值范圍;
(Ⅱ)求面積S2最大時,應怎樣設計材料的長和寬?
(Ⅲ)求面積(S1+2S2)最大時,應怎樣設計材料的長和寬?

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設D是函數y=f(x)定義域內的一個區間,若存在x0∈D,使f(x0)=﹣x0 , 則稱x0是f(x)的一個“次不動點”,也稱f(x)在區間D上存在次不動點.若函數f(x)=ax2﹣3x﹣a+ ![]() 在區間[1,4]上存在次不動點,則實數a的取值范圍是( )
在區間[1,4]上存在次不動點,則實數a的取值范圍是( )
A.(﹣∞,0)
B.(0, ![]() )
)
C.[ ![]() ,+∞)
,+∞)
D.(﹣∞, ![]() ]
]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=sin2xcos2x+sin22x﹣ ![]() .
.
(1)求函數f(x)的最小正周期及對稱中心;
(2)在△ABC中,角B為鈍角,角A,B,C的對邊分別為a、b、c,f( ![]() )=
)= ![]() ,且sinC=
,且sinC= ![]() sinA,S△ABC=4,求c的值.
sinA,S△ABC=4,求c的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x+ ![]() |﹣|x﹣
|﹣|x﹣ ![]() |;
|;
(1)作出函數f(x)的圖象;
(2)根據(1)所得圖象,填寫下面的表格:
性質 | 定義域 | 值域 | 單調性 | 奇偶性 | 零點 |
f(x) |
(3)關于x的方程f2(x)+m|f(x)|+n=0(m,n∈R)恰有6個不同的實數解,求n的取值范圍. 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a>0且a≠1,設命題p:函數y=loga(x-1)在(1,+∞)上單調遞減,命題q:曲線y=x2+(a-2)x+4與x軸交于不同的兩點.若“![]() p且q”為真命題,求實數a的取值范圍.
p且q”為真命題,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com