
【題目】下列計算曲線y=cosx(0≤x≤ ![]() )與坐標軸圍成的面積:
)與坐標軸圍成的面積:
(1)![]() cosxdx,(2)3
cosxdx,(2)3 ![]() cosxdx,(3)
cosxdx,(3) ![]() |cosx|dx,(4)面積為3.
|cosx|dx,(4)面積為3.
用的方法或結果正確的是 .
【答案】
(1)(2)、(3)、(4)
【解析】解:∵當0≤x≤ ![]() ,時,cosx≥0,當
,時,cosx≥0,當 ![]() ≤x≤
≤x≤ ![]() 時,cosx≤0,
時,cosx≤0,
∴曲線y=cosx(0≤x≤ ![]() )與坐標軸圍成的面積S=
)與坐標軸圍成的面積S= ![]() cosxdx﹣
cosxdx﹣ ![]() cosxdx,
cosxdx,
(1) ![]() cosxdx,錯誤,
cosxdx,錯誤,
(2)函數在0≤x≤ ![]() ,
, ![]() ≤x≤π,π≤x≤
≤x≤π,π≤x≤ ![]() 三段的面積相同,
三段的面積相同,
則S=3 ![]() cosxdx,正確
cosxdx,正確
(3) ![]() |cosx|dx,正確
|cosx|dx,正確
(4)面積為S=3 ![]() cosxdx=3sinx|
cosxdx=3sinx| ![]() =3(sin
=3(sin ![]() ﹣sin0)=3.
﹣sin0)=3.
正確,
所以答案是:(2)、(3)、(4);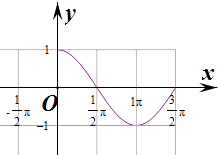
【考點精析】掌握定積分的概念是解答本題的根本,需要知道定積分的值是一個常數,可正、可負、可為零;用定義求定積分的四個基本步驟:①分割;②近似代替;③求和;④取極限.


科目:高中數學 來源: 題型:
【題目】如圖(1)所示,已知四邊形![]() 是由
是由![]() 和直角梯形
和直角梯形![]() 拼接而成的,其中
拼接而成的,其中![]() .且點
.且點![]() 為線段
為線段![]() 的中點,
的中點, ![]() ,
, ![]() .現將
.現將![]() 沿
沿![]() 進行翻折,使得二面角
進行翻折,使得二面角![]() 的大小為90°,得到圖形如圖(2)所示,連接
的大小為90°,得到圖形如圖(2)所示,連接![]() ,點
,點![]() 分別在線段
分別在線段![]() 上.
上.


(Ⅰ)證明: ![]() ;
;
(Ⅱ)若三棱錐![]() 的體積為四棱錐
的體積為四棱錐![]() 體積的
體積的![]() ,求點
,求點![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在四棱錐P﹣ABCD中,底面ABCD是邊長為2的正方形,平面PBC⊥底面ABCD,且 PB=PC= ![]() .
.
(Ⅰ)求證:AB⊥CP;
(Ⅱ)求點B到平面PAD的距離;
(Ⅲ)設面PAD與面PBC的交線為l,求二面角A﹣l﹣B的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙、丙三人參加了一家公司的招聘面試,面試合格者可正式簽約,甲表示只要面試合格就簽約.乙、丙則約定:兩人面試都合格就一同簽約,否則兩人都不簽約.設甲、乙、丙面試合格的概率分別是 ![]() ,
, ![]() ,
, ![]() ,且面試是否合格互不影響.求:
,且面試是否合格互不影響.求:
(1)至少有1人面試合格的概率;
(2)簽約人數ξ的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() x3﹣x2﹣
x3﹣x2﹣ ![]() x,則f(﹣a2)與f(﹣1)的大小關系為( )
x,則f(﹣a2)與f(﹣1)的大小關系為( )
A.f(﹣a2)≤f(﹣1)
B.f(﹣a2)<f(﹣1)
C.f(﹣a2)≥f(﹣1)
D.f(﹣a2)與f(﹣1)的大小關系不確定
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知一點在直線上從時刻t=0(s)開始以速度v(t)=t2﹣4t+3(m/s)運動,求:
(1)在t=4s時的位置;
(2)在t=4s的運動路程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com