
【題目】(1)證明:![]() ;
;
(2)證明:對任何正整數n,存在多項式函數![]() ,使得
,使得![]() 對所有實數x均成立,其中
對所有實數x均成立,其中![]() 均為整數,當n為奇數時,
均為整數,當n為奇數時,![]() ,當n為偶數時,
,當n為偶數時,![]() ;
;
(3)利用(2)的結論判斷![]() 是否為有理數?
是否為有理數?
【答案】(1)見解析;(2)見解析;(3)不是
【解析】
(1)![]() ,利用兩角和的正弦和二倍角公式,進行證明;(2)對
,利用兩角和的正弦和二倍角公式,進行證明;(2)對![]() 分奇偶,即
分奇偶,即![]() 和
和![]() 兩種情況,結合兩角和的余弦公式,積化和差公式,利用數學歸納法進行證明;(3)根據(2)的結論,將
兩種情況,結合兩角和的余弦公式,積化和差公式,利用數學歸納法進行證明;(3)根據(2)的結論,將![]() 表示出來,然后判斷其每一項都為無理數,從而得到答案.
表示出來,然后判斷其每一項都為無理數,從而得到答案.
(1)![]()
![]()
![]()
![]()
所以原式得證.
(2)![]() 為奇數時,
為奇數時,
![]() 時,
時,![]() ,其中
,其中![]() ,成立
,成立
![]() 時,
時,![]()
![]() ,其中
,其中![]() ,成立
,成立
![]() 時,
時,![]()
![]() ,其中
,其中![]() ,成立,
,成立,
則當![]() 時,
時,
![]()
![]()
所以得到
![]()
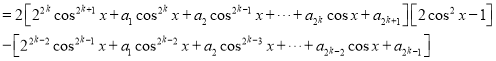
![]()
因為![]() 均為整數,所以
均為整數,所以![]() 也均為整數,
也均為整數,
故原式成立;
![]() 為偶數時,
為偶數時,
![]() 時,
時,![]() ,其中
,其中![]() ,
,
![]() 時,
時,![]()
![]() ,
,
其中![]() ,成立,
,成立,
![]() 時,
時,![]()
![]() ,
,
其中![]() ,成立,
,成立,
則當![]() 時,
時,
![]()
![]()
所以得到
![]()

![]() 其中
其中![]() ,
,
因為![]() 均為整數,所以
均為整數,所以![]() 也均為整數,
也均為整數,
故原式成立;
綜上可得:對任何正整數![]() ,存在多項式函數
,存在多項式函數![]() ,使得
,使得![]() 對所有實數
對所有實數![]() 均成立,其中
均成立,其中![]() ,
,![]() 均為整數,當
均為整數,當![]() 為奇數時,
為奇數時,![]() ,當
,當![]() 為偶數時,
為偶數時,![]() ;
;
(3)由(2)可得![]()
![]()
![]()
![]()
其中![]() 均為有理數,
均為有理數,
因為![]() 為無理數,所以
為無理數,所以![]() 均為無理數,
均為無理數,
故![]() 為無理數,
為無理數,
所以![]() 不是有理數.
不是有理數.


 能考試期末沖刺卷系列答案
能考試期末沖刺卷系列答案科目:高中數學 來源: 題型:
【題目】某超市計劃按月訂購一種酸奶,每天進貨量相同,進貨成本每瓶4元,售價每瓶6元,未售出的酸奶降價處理,以每瓶2元的價格當天全部處理完.根據往年銷售經驗,每天需求量與當天最高氣溫(單位:℃)有關.如果最高氣溫不低于25,需求量為500瓶;如果最高氣溫位于區間![]() ,需求量為300瓶;如果最高氣溫低于20,需求量為200瓶.為了確定六月份的訂購計劃,統計了前三年六月份各天的最高氣溫數據,得下面的頻數分布表:
,需求量為300瓶;如果最高氣溫低于20,需求量為200瓶.為了確定六月份的訂購計劃,統計了前三年六月份各天的最高氣溫數據,得下面的頻數分布表:
最高 氣溫 | [10, 15) | [15, 20) | [20, 25) | [25, 30) | [30, 35) | [35, 40) |
天數 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高氣溫位于各區間的頻率代替最高氣溫位于該區間的概率.
(1)求六月份這種酸奶一天的需求量X(單位:瓶)的分布列.
(2)設六月份一天銷售這種酸奶的利潤為Y(單位:元),當六月份這種酸奶一天的進貨量n(單位:瓶)為多少時,Y的數學期望達到最大值?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在幾何體ABCDE中,AB⊥平面BCE,且△BCE是正三角形,四邊形ABCD為正方形,F是線段CD上的中點,G是線段BE的中點,且AB=2.
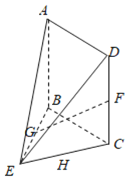
(1)求證:GF∥平面ADE;
(2)求三棱錐F–BGC的表面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,且過點
,且過點 .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)過橢圓![]() 的左焦點的直線
的左焦點的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,直線
兩點,直線![]() 過坐標原點且與直線
過坐標原點且與直線![]() 的斜率互為相反數.若直線
的斜率互為相反數.若直線![]() 與橢圓交于
與橢圓交于![]() 兩點且均不與點
兩點且均不與點![]() 重合,設直線
重合,設直線![]() 與
與![]() 軸所成的銳角為
軸所成的銳角為![]() ,直線
,直線![]() 與
與![]() 軸所成的銳角為
軸所成的銳角為![]() ,判斷
,判斷![]() 與
與![]() 的大小關系并加以證明.
的大小關系并加以證明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2017年5月,“一帶一路”沿線的20國青年評選出了中國“新四大發明”:高鐵、支付寶、共享單車和網購.2017年末,“支付寶大行動”用發紅包的方法刺激支付寶的使用.某商家統計前5名顧客掃描紅包所得金額分別為5.5元,2.1元,3.3元,5.9元,4.7元,商家從這5名顧客中隨機抽取3人贈送臺歷.
(1)求獲得臺歷是三人中至少有一人的紅包超過5元的概率;
(2)統計一周內每天使用支付寶付款的人數![]() 與商家每天的凈利潤
與商家每天的凈利潤![]() 元,得到7組數據,如表所示,并作出了散點圖.
元,得到7組數據,如表所示,并作出了散點圖.

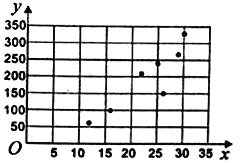
(i)直接根據散點圖判斷,![]() 與
與![]() 哪一個適合作為每天的凈利潤的回歸方程類型.(
哪一個適合作為每天的凈利潤的回歸方程類型.(![]() 的值取整數)
的值取整數)
(ii)根據(i)的判斷,建立![]() 關于
關于![]() 的回歸方程,并估計使用支付寶付款的人數增加到35時,商家當天的凈利潤.
的回歸方程,并估計使用支付寶付款的人數增加到35時,商家當天的凈利潤.
參考數據:
|
|
|
|
22.86 | 194.29 | 268.86 | 3484.29 |
附:對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為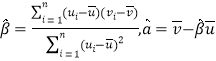 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com