已知函數 f(x)=3x2-6x-5.
(Ⅰ)求不等式 f(x)>4的解集;
(Ⅱ)若關于x的不等式f(x)<x2-(2a+6)x+a在x∈[1,3]上恒成立,求實數a的取值范圍;
(Ⅲ)設函數g(x)=f(x)-2x2+mx+5-6m(m∈R),記區間D=(1-m,m+15),若不等式g(x)<0的解集為M,且D∩M=∅,求實數m的取值范圍.
【答案】
分析:(I)根據已知中函數解析式,化簡不等式 f(x)>4,進而根據二次不等式的解法,可得不等式 f(x)>4的解集;
(Ⅱ)根據已知中函數解析式,化簡不等式f(x)<x
2-(2a+6)x+a,根據二次函數的圖象及性質,可得函數在區間[1,3]上恒成立,即函數在區間兩端點的函數值均為負,構造不等式組,可得實數a的取值范圍;
(Ⅲ)根據已知中函數解析式,化簡不等式g(x)<0,結合D=(1-m,m+15),且D∩M=∅,分類討論求出滿足條件的實數m的取值范圍.
解答:解:(I)不等式 f(x)>4
即3x
2-6x-9>0
解得x>3,或x<-1
∴不等式 f(x)>4的解集為(-∞,-1)∪(3,+∞)
(II)若不等式f(x)<x
2-(2a+6)x+a在x∈[1,3]上恒成立,
即不等式2x
2+2ax-5-a<0在x∈[1,3]上恒成立,
令h(x)=2x
2+2ax-5-a
則
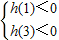
,即
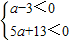
解得a<
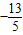
(III)∵g(x)=f(x)-2x
2+mx+5-6m=x
2+(m-6)x-6m
∴當g(x)=0時,x=6,或x=-m
當-m>6,即m<-6時,不等式g(x)<0的解集M=(6,-m)
∵D=(1-m,m+15),且D∩M=∅,
∴
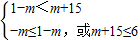
,
∴-7<m<-6
當-m=6,即m=-6時,不等式g(x)<0的解集M=∅
滿足D∩M=∅,
當-m<6,即m>-6時,不等式g(x)<0的解集M=(-m,6)
∵D=(1-m,m+15),且D∩M=∅,
∴
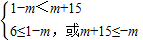
,
∴-6<m≤-5
綜上可得實數m的取值范圍為-7<m≤-5
點評:本題考查的知識點是函數的恒成立問題,一元二次不等式的解法,函數的交集運算,其中熟練掌握二次函數的圖象和性質并能用之解答一元二次不等式問題是解答的關鍵.

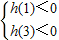 ,即
,即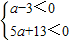
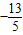
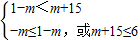 ,
,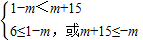 ,
,

 陽光課堂課時作業系列答案
陽光課堂課時作業系列答案