【題目】設等差數列{an}滿足a3=5，a10=﹣9．
（1）求數列{an}的通項公式；
（2）求Sn的最大值及其相應的n的值．
新思維假期作業暑假吉林大學出版社系列答案
藍天教育暑假優化學習系列答案科目：高中數學 來源： 題型：
【題目】下列命題中 ①若loga3＞logb3，則a＞b；
②函數f（x）=x2﹣2x+3，x∈[0，+∞）的值域為[2，+∞）；
③設g（x）是定義在區間[a，b]上的連續函數．若g（a）=g（b）＞0，則函數g（x）無零點；
④函數 
既是奇函數又是減函數．
其中正確的命題有
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}是等差數列，若a9+3a11＜0，a10a11＜0，且數列{an}的前n項和Sn有最大值，那么Sn取得最小正值時n等于（ ）
A.20
B.17
C.19
D.21
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
已知直線
的參數方程為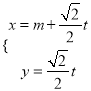
（
為參數），以坐標原點
為極點，以
軸正半軸為極軸，建立極坐標系，曲線
的極坐標方程為
，且曲線
的左焦點
在直線上．
（1）若直線
與曲線
交于
兩點，求
的值；
（2）設曲線
的內接矩形的周長為
，求
的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知遞增等比數列{an}的第三項、第五項、第七項的積為512，且這三項 分別減去1，3，9后成等差數列．
（1）求{an}的首項和公比；
（2）設Sn=a12+a22+…+an2 ， 求Sn ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）是定義在R上的偶函數，且在區間[0，+∞）上單調遞增，若實數a滿足f（log4a）+f（lo 
a）≤2f（1），則實數a的取值范圍是 ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】用an表示自然數n的所有因數中最大的那個奇數，例如：9的因數有1，3，9，則a9=9；10的因數有1，2，5，10，則a10=5，記數列{an}的前n項和為Sn ， 則S 
= ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列an的首項a1=2，且an=2an﹣1﹣1（nN+ ， n≥2）．
（1）求數列{an}的通項公式；
（2）求數列{nan﹣n}的前n項和Sn ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知二次函數f（x）=ax2+x（a∈R，a≠0）．
（1）當a＞0時，用作差法證明：f（ 
）＜ 
[f（x1）+f（x2）]；
（2）已知當x∈[0，1]時，|f（x）|≤1恒成立，試求實數a的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
