
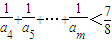 .
.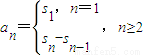 進行代換,要注意n=1和n≥2的討論,在得到an=2an-1+2(-1)n-1,可以設
進行代換,要注意n=1和n≥2的討論,在得到an=2an-1+2(-1)n-1,可以設 構造一個等比數列;
構造一個等比數列;
 }是以
}是以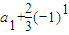 為首項,公比為2的等比數列.
為首項,公比為2的等比數列.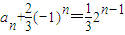 ∴
∴
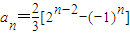 .
. =
=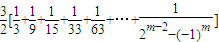 =
=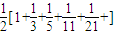
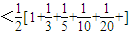 =
= =
= =
=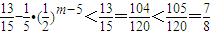 .
.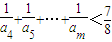 (m>4).
(m>4).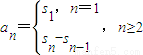 的應用是高考考查的重點,要能熟練的應用.另外本題(2)中對構造數列的考查較好,(3)中不等式證明中的放縮是一個難點,需要有扎實的基本功及一定的運算能力,對運算放縮能力要求較高.
的應用是高考考查的重點,要能熟練的應用.另外本題(2)中對構造數列的考查較好,(3)中不等式證明中的放縮是一個難點,需要有扎實的基本功及一定的運算能力,對運算放縮能力要求較高. 

 開心蛙狀元作業系列答案
開心蛙狀元作業系列答案 課時掌控隨堂練習系列答案
課時掌控隨堂練習系列答案 一課一練一本通系列答案
一課一練一本通系列答案 浙江之星學業水平測試系列答案
浙江之星學業水平測試系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com