
分析 (1)由題意,列出關(guān)于a,b,c的方程組,解得即可,則橢圓方程可求;
(2)設(shè)直線(xiàn)l:x=my+n點(diǎn)M(x1,y1),N(x2,y2),與橢圓方程聯(lián)立,利用根與系數(shù)的關(guān)系及$\overrightarrow{AM}•\overrightarrow{AN}$=0,求出x=m(y+$\frac{3}{14}$)+$\frac{1}{7}$,即可得到直線(xiàn)過(guò)定點(diǎn).
解答 解:(1)設(shè)橢圓的方程為:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),則由已知可得:$\left\{\begin{array}{l}{\frac{1}{{a}^{2}}+\frac{\frac{9}{4}}{{b}^{2}}=1}\\{{a}^{2}={b}^{2}+{c}^{2}}\\{\frac{\frac{3}{2}}{1+c}=\frac{3}{4}}\end{array}\right.$,解得a=2,b=$\sqrt{3}$,c=1,
則橢圓的方程為:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,
(2)設(shè)直線(xiàn)l:x=my+n點(diǎn)M(x1,y1),N(x2,y2).直線(xiàn)l與橢圓C的方程聯(lián)立,消去x得,(4+3m2)y2+8mny+3m2-12=0,
∴y1+y2=-$\frac{6mn}{3{m}^{2}+4}$,y1y2=$\frac{3{n}^{2}-12}{3{m}^{2}+4}$,①
同理可得:x1+x2=$\frac{8n}{3{m}^{2}+4}$,x1x2=$\frac{4{n}^{2}-12{m}^{2}}{3{m}^{2}+4}$,②,
又由∠MAN=90°,則$\overrightarrow{AM}•\overrightarrow{AN}$=0,
∴(x1-1,y1-$\frac{3}{2}$)•(x2-1,y2-$\frac{3}{2}$)=x1x2-(x1+x2)+y1y2-$\frac{3}{2}$(y1+y2)+$\frac{13}{4}$=0③
將①②代入③整理得:3($\frac{3}{2}$m+n)2+4(n-1)2-9m2-3=0,
也就是3($\frac{3}{2}$m+n-1)($\frac{3}{2}$m+n+1)+4(n-1-$\frac{3}{2}$m)(n-1+$\frac{3}{2}$m)=0,
由于點(diǎn)A不在直線(xiàn)l上,則$\frac{3}{2}$m+n-1≠0則,
3($\frac{3}{2}$m+n+1)+4(n-1-$\frac{3}{2}$m)=0,整理n=$\frac{2+3m}{14}$,
則x=my+n=my+$\frac{2+3m}{14}$=m(y+$\frac{3}{14}$)+$\frac{1}{7}$,
所以直線(xiàn)l過(guò)定點(diǎn)($\frac{1}{7}$,-$\frac{3}{14}$)
點(diǎn)評(píng) 本題考查橢圓標(biāo)準(zhǔn)方程的求法,考查了直線(xiàn)與圓錐曲線(xiàn)位置關(guān)系的應(yīng)用,訓(xùn)練了存在性問(wèn)題的求解方法,考查了數(shù)形結(jié)合的思想、推理能力和計(jì)算能力,屬難題.


 黃岡小狀元解決問(wèn)題天天練系列答案
黃岡小狀元解決問(wèn)題天天練系列答案 三點(diǎn)一測(cè)快樂(lè)周計(jì)劃系列答案
三點(diǎn)一測(cè)快樂(lè)周計(jì)劃系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源:2017屆安徽合肥一中高三上學(xué)期月考一數(shù)學(xué)(理)試卷(解析版) 題型:選擇題
若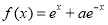 為偶函數(shù),則
為偶函數(shù),則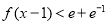 的解集為( )
的解集為( )
A.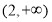 B.
B.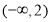
C.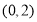 D.
D.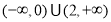
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2016-2017學(xué)年河北正定中學(xué)高二上月考一數(shù)學(xué)(理)試卷(解析版) 題型:選擇題
在斜△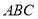 中,角
中,角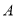 ,
,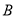 ,
,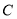 所對(duì)的邊長(zhǎng)分別為
所對(duì)的邊長(zhǎng)分別為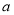 ,
,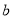 ,
,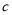 ,
,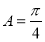 ,
,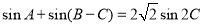 ,且△
,且△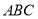 的面積為1,則
的面積為1,則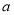 的值為( )
的值為( )
A. B.
B.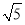 C.
C.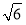 D.
D.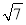
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 2 | B. | 3 | C. | 4 | D. | 1 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | π | B. | $\frac{π}{2}$ | C. | $\frac{3π}{8}$ | D. | $\frac{π}{16}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
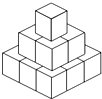 把14個(gè)棱長(zhǎng)為1的正方體,在地面上堆疊成如圖所示的幾何體,然后將露出的表面部分染成紅色.那么紅色部分的面積為( )
把14個(gè)棱長(zhǎng)為1的正方體,在地面上堆疊成如圖所示的幾何體,然后將露出的表面部分染成紅色.那么紅色部分的面積為( )| A. | .21 | B. | .24 | C. | .33 | D. | .37 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com