
| 2 |
| 2 |
| 2 |
| 2 |


 名師點撥卷系列答案
名師點撥卷系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
(1)設A={1,2,3,4},B={3,4,5,6,7,8,9},對應法則f:x→2x+1;
(2)設A=N *,B={0,1},對應法則f:x→x除以2得到的余數;
(3)設X={1,2,3,4},Y={1,![]() ,
,![]() ,
,![]() },f:x→x取倒數?;
},f:x→x取倒數?;
(4)A={(x,y)||x|<2,x+y<3,x∈Z,y∈N},B={0,1,2},f:(x,y)→x+y;
(5)A={x|x>2,x∈N},B=N,f:x→小于x的最大質數;
(6)A=N,B={0,1,2},f:x→x被3除所得余數.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年浙江省高三上學期期中考試理科數學卷 題型:解答題
(本小題滿分15分)
已知以點 為圓心的圓與x軸交于點O、A,與y軸交于點O、B,其中O為原點。
為圓心的圓與x軸交于點O、A,與y軸交于點O、B,其中O為原點。
(Ⅰ)求證:△AOB的面積為定值;
(Ⅱ)設直線2x+y-4=0與圓C交于點M、N,若 ,求圓C的方程;
,求圓C的方程;
(Ⅲ)在(Ⅱ)的條件下,設P、Q分別是直線l:x+y+2=0和圓C的動點,求 的最小值及此時點P的坐標。
的最小值及此時點P的坐標。
查看答案和解析>>
科目:高中數學 來源:2010-2011學年浙江省高三上學期期中考試理科數學卷 題型:解答題
(本小題滿分15分)
已知以點 為圓心的圓與x軸交于點O、A,與y軸交于點O、B,其中O為原點。
為圓心的圓與x軸交于點O、A,與y軸交于點O、B,其中O為原點。
(Ⅰ)求證:△AOB的面積為定值;
(Ⅱ)設直線2x+y-4=0與圓C交于點M、N,若 ,求圓C的方程;
,求圓C的方程;
(Ⅲ)在(Ⅱ)的條件下,設P、Q分別是直線l:x+y+2=0和圓C的動點,求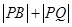 的最小值及此時點P的坐標。
的最小值及此時點P的坐標。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com