
①由“若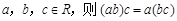 ”類比“若
”類比“若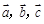 為三個向量,則
為三個向量,則 ”;②設圓
”;②設圓 與坐標軸的4個交點分別為A (x1,0)、B (x2,0)、C (0,y1)、D (0,y2),則
與坐標軸的4個交點分別為A (x1,0)、B (x2,0)、C (0,y1)、D (0,y2),則 ;③在平面內“三角形的兩邊之和大于第三邊”類比在空間中“四面體的任意三個面的面積之和大于第四個面的面積”;④在實數列
;③在平面內“三角形的兩邊之和大于第三邊”類比在空間中“四面體的任意三個面的面積之和大于第四個面的面積”;④在實數列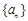 中,已知a1 = 0,
中,已知a1 = 0,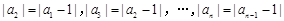 ,則
,則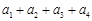 的最大值為2.上述四個推理中,得出的結論正確的是_____________(寫出所有正確結論的序號).
的最大值為2.上述四個推理中,得出的結論正確的是_____________(寫出所有正確結論的序號).
②③④
解析試題分析:①由“若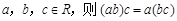 ”類比“若
”類比“若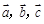 為三個向量,則
為三個向量,則 ”,此結論錯誤,
”,此結論錯誤, 表示與
表示與 共線的向量,
共線的向量, 表示與
表示與 共線的向量,不一定相等;②設圓
共線的向量,不一定相等;②設圓 與坐標軸的4個交點分別為A (x1,0)、B (x2,0)、C (0,y1)、D (0,y2),則
與坐標軸的4個交點分別為A (x1,0)、B (x2,0)、C (0,y1)、D (0,y2),則 ,正確。因為
,正確。因為 ,同理,
,同理,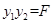 ,所以
,所以 ;③在平面內“三角形的兩邊之和大于第三邊”類比在空間中“四面體的任意三個面的面積之和大于第四個面的面積”,正確;④在實數列
;③在平面內“三角形的兩邊之和大于第三邊”類比在空間中“四面體的任意三個面的面積之和大于第四個面的面積”,正確;④在實數列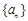 中,已知a1 = 0,
中,已知a1 = 0,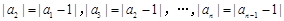 ,則
,則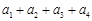 的最大值為2,正確。記
的最大值為2,正確。記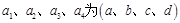 ,
,
則所有的情況為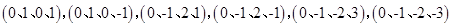 共六種,易得
共六種,易得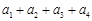 的最大值為2。
的最大值為2。
考點:類比推理;平面向量數量積的性質;圓的一般式方程;數列的應用。
點評:本題考查類比推理歸納推理,本題解題的關鍵是正確理解類比和歸納的含義,注意本題所包含的四個命題都要正確解出才能做對本題.


科目:高中數學 來源: 題型:填空題
以下命題:①若 ,則
,則 ∥
∥ ;②
;② =(-1,1)在
=(-1,1)在 =(3,4)方向上的投影為
=(3,4)方向上的投影為 ;③若△ABC中,a="5,b" ="8,c" =7,則
;③若△ABC中,a="5,b" ="8,c" =7,則 ·
· =20;④若非零向量
=20;④若非零向量 、
、 滿足
滿足 ,則
,則 .其中所有真命題的標號是
.其中所有真命題的標號是
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
已知α,β表示兩個不同的平面,m為平面α內的一條直線,則“α⊥β”是“m⊥β”的________條件.(填充分必要條件,充分不必要條件,必要不充分條件,既不充分又不必要條件之一)
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
下列四個命題:
①若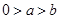 ,則
,則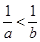 ;
;
②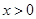 ,
,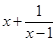 的最小值為
的最小值為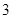 ;
;
③橢圓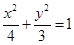 比橢圓
比橢圓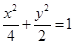 更接近于圓;
更接近于圓;
④設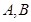 為平面內兩個定點,若有
為平面內兩個定點,若有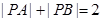 ,則動點
,則動點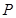 的軌跡是橢圓;
的軌跡是橢圓;
其中真命題的序號為________________.(寫出所有真命題的序號)
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
給出下列四個命題:
(1)方程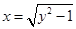 表示雙曲線的一部分;
表示雙曲線的一部分;
(2)動點到兩個定點的距離之和為定長,則動點的軌跡為橢圓;
(3)動點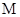 與點
與點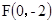 的距離比它到直線
的距離比它到直線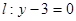 的距離小1的軌跡方程是
的距離小1的軌跡方程是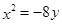 ;
;
(4)若雙曲線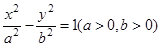 的兩條漸近線將平面劃分為“上、下、左、右”四個區域(不含邊界),若點
的兩條漸近線將平面劃分為“上、下、左、右”四個區域(不含邊界),若點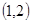 在“上”區域內,則雙曲線的離心率
在“上”區域內,則雙曲線的離心率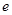 的取值范圍是
的取值范圍是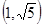 .其中所有正確命題的序號是 .
.其中所有正確命題的序號是 .
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
給出下列命題:
①存在實數 ,使得
,使得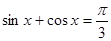 ;
;
②函數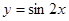 的圖象向右平移
的圖象向右平移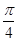 個單位,得到
個單位,得到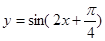 的圖象;
的圖象;
③函數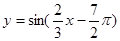 是偶函數;
是偶函數;
④已知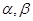 是銳角三角形ABC的兩個內角,則
是銳角三角形ABC的兩個內角,則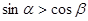 。
。
其中正確的命題的個數為
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
若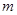 、
、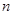 為兩條不重合的直線,
為兩條不重合的直線, 、
、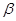 為兩個不重合的平面,給出下列命題
為兩個不重合的平面,給出下列命題
①若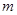 、
、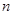 都平行于平面
都平行于平面 ,則
,則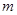 、
、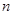 一定不是相交直線;②若
一定不是相交直線;②若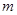 、
、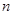 為都垂直于平面
為都垂直于平面 ,則
,則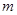 、
、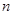 一定是平行直線;③已知
一定是平行直線;③已知 、
、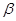 互相垂直,
互相垂直,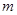 、
、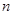 互相垂直,若
互相垂直,若 ;④
;④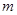 、
、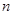 在平面
在平面 內的射影互相垂直,則
內的射影互相垂直,則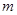 、
、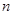 互相垂直。其中的假命題的序號是 .
互相垂直。其中的假命題的序號是 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com