設常數a≥0,函數f(x)=x-ln2x+2alnx-1
(1)令g(x)=xf'(x)(x>0),求g(x)的最小值,并比較g(x)的最小值與0的大小;
(2)求證:f(x)在(0,+∞)上是增函數;
(3)求證:當x>1時,恒有x>ln2x-2alnx+1.
【答案】
分析:(1)依題意求出g(x)的表示式,用導數研究其單調性求出其最小值再與0比較;
(2)利用(1)的結論進行證明,判斷時要求注意研究的區間是(0,+∞)這一特征;
(3)由(2)的結論知只須證明f(1)非負即可.
解答:解:(Ⅰ)∵f(x)=x-(lnx)(lnx)+2alnx-1,x∈(0,+∞)
∴
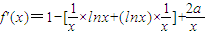
,=
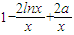
,(2分)
∴g(x)=xf'(x)=x-2lnx+2a,x∈(0,+∞)
∴
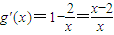
,令g'(x)=0,得x=2,(4分)
列表如下:
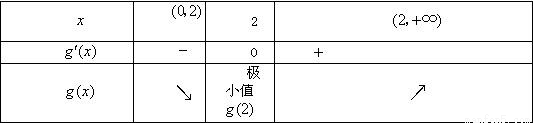
∴g(x)在x=2處取得極小值g(2)=2-2ln2+2a,
即g(x)的最小值為g(2)=2-2ln2+2a.(6分)g(2)=2(1-ln2)+2a,
∵ln2<1,∴1-ln2>0,又a≥0,
∴g(2)>0
證明(Ⅱ)由(Ⅰ)知,g(x)的最小值是正數,
∴對一切x∈(0,+∞),恒有g(x)=xf'(x)>0
從而當x>0時,恒有f'(x)>0
故f(x)在(0,+∞)上是增函數
證明(Ⅲ)由(Ⅱ)知:f(x)在(0,+∞)上是增函數,
∴當x>1時,f(x)>f(1)
又f(1)=1-ln
21+2aln1-1=0
∴f(x)>0,即x-1-ln
2x+2alnx>0
∴x>ln
2x-2alnx+1
故當x>1時,恒有x>ln
2x-2alnx+1
點評:考查用導數法求最值,本題三個小題后一個以前一個的結論為基礎做題,在遇到這一類題時,即使前一問的結論沒有證出來,也可以依據前一問的結論為論據求解后一問的問題,請讀者注意這個經驗.

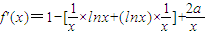 ,=
,=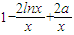 ,(2分)
,(2分)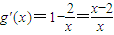 ,令g'(x)=0,得x=2,(4分)
,令g'(x)=0,得x=2,(4分)


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案