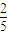從數字1、2、3、4、5中任取3個,組成沒有重復數字的三位數,則:
(1)這個三位數是5的倍數的概率是 .
(2)這個三位數大于400的概率是 .
【答案】
分析:(1)本題可以應用等可能時間來考慮,1,2,3,4,5這五個數字,出現在個位上的概率是等可能的,只有最后一位上是數字5,才能是5的倍數,根據等可能事件的概率得到結果.
(2)本題是一個古典概型,試驗發生包含的事件是從數字1、2、3、4、5中任取3個,組成沒有重復數字的三位數,滿足條件事件是這個三位數大于400,當首位是4和5時,都能使得數字大于400,寫出結果數,做比值得到概率.
解答:解:(1)本題可以應用等可能時間來考慮,
1,2,3,4,5這五個數字,出現在個位上的概率是等可能的,
只有最后一位上是數字5,才能是5的倍數,
∴這個三位數是5的倍數的概率是
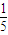
(2)由題意知,本題是一個古典概型,
試驗發生包含的事件是從數字1、2、3、4、5中任取3個,
組成沒有重復數字的三位數,共有A
53=120,
滿足條件的事件是這個三位數大于400,當首位是4和5時,都能使得數字大于400,
共有A
22A
42=48種結果,
根據古典概型公式得到P=
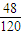
=
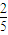
故答案為:(1)
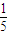
,(2)
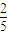 點評:
點評:數字問題是概率中經常出現的題目,一般可以列舉出要求的事件,古典概型要求能夠列舉出所有事件和發生事件的個數,而不能列舉的可以借助于排列數和組合數來表示.

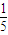
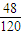 =
=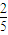
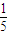 ,(2)
,(2)