
【題目】近來天氣變化無常,陡然升溫、降溫幅度大于![]() 的天氣現象出現增多.陡然降溫幅度大于
的天氣現象出現增多.陡然降溫幅度大于![]() 容易引起幼兒傷風感冒疾病.為了解傷風感冒疾病是否與性別有關,在某婦幼保健院隨機對人院的
容易引起幼兒傷風感冒疾病.為了解傷風感冒疾病是否與性別有關,在某婦幼保健院隨機對人院的![]() 名幼兒進行調查,得到了如下的列聯表,若在全部
名幼兒進行調查,得到了如下的列聯表,若在全部![]() 名幼兒中隨機抽取
名幼兒中隨機抽取![]() 人,抽到患傷風感冒疾病的幼兒的概率為
人,抽到患傷風感冒疾病的幼兒的概率為![]() ,
,
(1)請將下面的列聯表補充完整;
患傷風感冒疾病 | 不患傷風感冒疾病 | 合計 | |
男 | 25 | ||
女 | 20 | ||
合計 | 100 |
(2)能否在犯錯誤的概率不超過![]() 的情況下認為患傷風感冒疾病與性別有關?說明你的理由;
的情況下認為患傷風感冒疾病與性別有關?說明你的理由;
(3)已知在患傷風感冒疾病的![]() 名女性幼兒中,有
名女性幼兒中,有![]() 名又患黃痘病.現在從患傷風感冒疾病的
名又患黃痘病.現在從患傷風感冒疾病的![]() 名女性中,選出
名女性中,選出![]() 名進行其他方面的排查,記選出患黃痘病的女性人數為
名進行其他方面的排查,記選出患黃痘病的女性人數為![]() ,求
,求![]() 的分布列以及數學期望.下面的臨界值表供參考:
的分布列以及數學期望.下面的臨界值表供參考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
參考公式: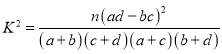 ,其中
,其中![]()
【答案】(1)見解析,(2) 不能在犯錯誤的概率不超過![]() 的情況下認為患傷風感冒疾病與性別有美.(3)分布列見解析,
的情況下認為患傷風感冒疾病與性別有美.(3)分布列見解析,![]()
【解析】
(1)根據在全部![]() 名幼兒中隨機抽取
名幼兒中隨機抽取![]() 人,抽到患傷風感冒疾病的幼兒的概率為
人,抽到患傷風感冒疾病的幼兒的概率為![]() ,可以求出患傷風感冒疾病的幼兒的數量,這樣可以補充完成列聯表;
,可以求出患傷風感冒疾病的幼兒的數量,這樣可以補充完成列聯表;
(2)代入公式求出![]() 的值,根據所給的表寫出結論;
的值,根據所給的表寫出結論;
(3) 根據題意,![]() 的值可能為
的值可能為![]() .分別求出相應的概率值,列出分布列,計算出數學期望即可.
.分別求出相應的概率值,列出分布列,計算出數學期望即可.
(1)列聯表補充如下;
患傷風感冒疾病 | 不患傷風感冒疾病 | 合計 | |
男 |
|
|
|
女 |
|
|
|
合計 |
|
|
|
![]() 計
計![]() 算的觀測值為
算的觀測值為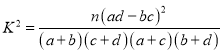
![]() ,
,
所以不能在犯錯誤的概率不超過![]() 的情況下認為患傷風感冒疾病與性別有美.
的情況下認為患傷風感冒疾病與性別有美.
(3)根據題意,![]() 的值可能為
的值可能為![]() .
.
則![]() ,
,![]() ,
,
故![]() 的分布列如下:
的分布列如下:
|
|
|
|
|
|
|
|
故![]() 的數學期望:
的數學期望:![]() .
.


科目:高中數學 來源: 題型:
【題目】![]() 是定義在
是定義在![]() 上的奇函數,對
上的奇函數,對![]() ,均有
,均有![]() ,已知當
,已知當![]() 時,
時, ![]() ,則下列結論正確的是( )
,則下列結論正確的是( )
A. ![]() 的圖象關于
的圖象關于![]() 對稱 B.
對稱 B. ![]() 有最大值1
有最大值1
C. ![]() 在
在![]() 上有5個零點 D. 當
上有5個零點 D. 當![]() 時,
時, ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位共有老年人120人,中年人360人,青年人n人,為調查身體健康狀況,需要從中抽取一個容量為m的樣本,用分層抽樣的方法進行抽樣調查,樣本中的中年人為6人,則n和m的值不可以是下列四個選項中的哪組( )
A.n=360,m=14B.n=420,m=15C.n=540,m=18D.n=660,m=19
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年雙十一落下帷幕,天貓交易額定格在268(單位:十億元)人民幣(下同),再創新高,比去年218(十億元)多了50(十億元),這些數字的背后,除了是消費者買買買的表現,更是購物車里中國新消費的奇跡,為了研究歷年銷售額的變化趨勢,一機構統計了2010年到2019年天貓雙十一的銷售額數據![]() (單位:十億元).繪制如下表1:
(單位:十億元).繪制如下表1:
表1
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
編號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
銷售額 | 0.9 | 8.7 | 22.4 | 41 | 65 | 94 | 132.5 | 172.5 | 218 | 268 |
根據以上數據繪制散點圖,如圖所示.
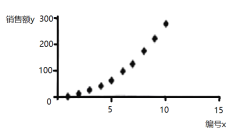
(1)根據散點圖判斷,![]() 與
與![]() 哪一個適宜作為銷售額
哪一個適宜作為銷售額![]() 關于
關于![]() 的回歸方程類型?(給出判斷即可,不必說明理由)
的回歸方程類型?(給出判斷即可,不必說明理由)
(2)根據(1)的判斷結果及下表中的數據,建立![]() 關于
關于![]() 的回歸方程,并預測2020年天貓雙十一銷售額;(注:數據保留小數點后一位)
的回歸方程,并預測2020年天貓雙十一銷售額;(注:數據保留小數點后一位)
(3)把銷售額超過10(十億元)的年份叫“暢銷年”,把銷售額超過100(十億元)的年份叫“狂歡年”,從2010年到2019年這十年的“暢銷年”中任取3個,求取到的“狂歡年”個數![]() 的分布列與期望.
的分布列與期望.
參考數據:![]() .
.
|
|
|
|
|
|
參考公式:對于一組數據![]() ,
,![]() ,…,
,…,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計公式分別為
的斜率和截距的最小二乘估計公式分別為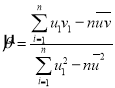 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在貫徹中共中央、國務院關于精準扶貧政策的過程中,某單位在某市定點幫扶某村![]() 戶貧困戶.為了做到精準幫扶,工作組對這
戶貧困戶.為了做到精準幫扶,工作組對這![]() 戶村民的年收入情況、危舊房情況、患病情況等進行調查,并把調查結果轉化為各戶的貧困指標
戶村民的年收入情況、危舊房情況、患病情況等進行調查,并把調查結果轉化為各戶的貧困指標![]() .將指標
.將指標![]() 按照
按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成五組,得到如圖所示的頻率分布直方圖.規定若
分成五組,得到如圖所示的頻率分布直方圖.規定若![]() ,則認定該戶為“絕對貧困戶”,否則認定該戶為“相對貧困戶”;當
,則認定該戶為“絕對貧困戶”,否則認定該戶為“相對貧困戶”;當![]() 時,認定該戶為“亟待幫住戶”.工作組又對這
時,認定該戶為“亟待幫住戶”.工作組又對這![]() 戶家庭的受教育水平進行評測,家庭受教育水平記為“良好”與“不好”兩種.
戶家庭的受教育水平進行評測,家庭受教育水平記為“良好”與“不好”兩種.

(1)完成下面的列聯表,并判斷是否有![]() 的把握認為絕對貧困戶數與受教育水平不好有關:
的把握認為絕對貧困戶數與受教育水平不好有關:
受教育水平良好 | 受教育水平不好 | 總計 | |
絕對貧困戶 |
| ||
相對貧困戶 |
| ||
總計 |
|
(2)上級部門為了調查這個村的特困戶分布情況,在貧困指標處于![]() 的貧困戶中,隨機選取兩戶,用
的貧困戶中,隨機選取兩戶,用![]() 表示所選兩戶中“亟待幫助戶”的戶數,求
表示所選兩戶中“亟待幫助戶”的戶數,求![]() 的分布列和數學期望
的分布列和數學期望![]() .
.
附: ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】氣象意義上從春季進入夏季的標志為連續5天的日平均溫度均不低于22℃.現有甲、乙、丙三地連續5天的日平均溫度的記錄數據:(記錄數據都是正整數)
①甲地5個數據的中位數為24,眾數為22;
②乙地5個數據的中位數為27,總體均值為24;
③丙地5個數據中有一個數據是32,總體均值為26,總體方差為10.8.
則肯定進入夏季的地區有_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() ,的焦點為
,的焦點為![]() ,過點
,過點![]() 的直線
的直線![]() 的斜率為
的斜率為![]() ,與拋物線
,與拋物線![]() 交于
交于![]() ,
,![]() 兩點,拋物線在點
兩點,拋物線在點![]() ,
,![]() 處的切線分別為
處的切線分別為![]() ,
,![]() ,兩條切線的交點為
,兩條切線的交點為![]() .
.
(1)證明:![]() ;
;
(2)若![]() 的外接圓
的外接圓![]() 與拋物線
與拋物線![]() 有四個不同的交點,求直線
有四個不同的交點,求直線![]() 的斜率的取值范圍.
的斜率的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).以原點
為參數).以原點![]() 為極點,以
為極點,以![]() 軸為非負半軸為極軸建立極坐標系,兩坐標系相同的長度單位.圓
軸為非負半軸為極軸建立極坐標系,兩坐標系相同的長度單位.圓![]() 的方程為
的方程為![]() 被圓
被圓![]() 截得的弦長為
截得的弦長為![]() .
.
(Ⅰ)求實數![]() 的值;
的值;
(Ⅱ)設圓![]() 與直線
與直線![]() 交于點
交于點![]() ,若點
,若點![]() 的坐標為
的坐標為![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com