
【題目】如圖,點![]() 在以
在以![]() 為直徑的上運動,
為直徑的上運動,![]() 平面
平面![]() ,且
,且![]() ,點
,點![]() 、
、![]() 分別是
分別是![]() 、
、![]() 的中點.
的中點.
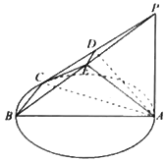
(1)求證:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求平面
,求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
科目:高中數學 來源: 題型:
【題目】某市勞動部門堅持就業優先,釆取多項措施加快發展新興產業,服務經濟,帶來大量就業崗位,據政府工作報告顯示,截至2018年末,全市城鎮新增就業21.9萬人,創歷史新高.城鎮登記失業率為4.2%,比上年度下降0.73個百分點,處于近20年來的最低水平.
(1)現從該城鎮適齡人群中抽取100人,得到如下列聯表:
失業 | 就業 | 合計 | |
男 | 3 | 62 | 65 |
女 | 2 | 33 | 35 |
合計 | 5 | 95 | 100 |
根據聯表判斷是否有99%的把握認為失業與性別有關?
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |

(2)調查顯示,新增就業人群中,新興業態,民營經濟,大型國企對就業支撐作用不斷增強,其崗位比例為2∶5∶3,現要抽取一個樣本容量為50的樣本,則這三種崗位應該各抽取多少人?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),曲線
為參數),曲線![]() :
: ![]() .以
.以![]() 為極點,
為極點, ![]() 軸的非負半軸為極軸,與直角坐標系
軸的非負半軸為極軸,與直角坐標系![]() 取相同的長度單位,建立極坐標系.
取相同的長度單位,建立極坐標系.
(1)求曲線![]() 的極坐標方程;
的極坐標方程;
(2)射線![]() (
(![]() )與曲線
)與曲線![]() 的異于極點的交點為
的異于極點的交點為![]() ,與曲線
,與曲線![]() 的交點為
的交點為![]() ,求
,求![]() .
.
【答案】(1) ![]() 的極坐標方程為
的極坐標方程為![]() ,
, ![]() 的極坐標方程為
的極坐標方程為![]() ;(2)
;(2) ![]() .
.
【解析】試題分析:(1)先根據三角函數平方關系消參數得曲線![]() ,再根據
,再根據![]() 將曲線
將曲線![]() 的
的![]() 極坐標方程;(2)將
極坐標方程;(2)將![]() 代人曲線
代人曲線![]() 的極坐標方程,再根據
的極坐標方程,再根據![]() 求
求![]() .
.
試題解析:(1)曲線![]() 的參數方程
的參數方程![]() (
(![]() 為參數)
為參數)
可化為普通方程![]() ,
,
由![]() ,可得曲線
,可得曲線![]() 的極坐標方程為
的極坐標方程為![]() ,
,
曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(2)射線![]() (
(![]() )與曲線
)與曲線![]() 的交點
的交點![]() 的極徑為
的極徑為![]() ,
,
射線![]() (
(![]() )與曲線
)與曲線![]() 的交點
的交點![]() 的極徑滿足
的極徑滿足![]() ,解得
,解得![]() ,
,
所以![]() .
.
【題型】解答題
【結束】
23
【題目】設函數![]() .
.
(1)設![]() 的解集為
的解集為![]() ,求集合
,求集合![]() ;
;
(2)已知![]() 為(1)中集合
為(1)中集合![]() 中的最大整數,且
中的最大整數,且![]() (其中
(其中![]() ,
,![]() ,
,![]() 為正實數),求證:
為正實數),求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】畢達哥拉斯樹是由畢達哥拉斯根據“勾股定理”所畫出來的一個可以無限重復的圖形,也叫“勾股樹”,其是由一個等腰直角三角形分別以它的每一條邊向外作正方形而得到.圖1所示是第1代“勾股樹”,重復圖1的作法,得到第2代“勾股樹”(如圖2),如此繼續.若“勾股樹”上共得到8191個正方形,設初始正方形的邊長為1,則最小正方形的邊長為( )
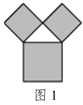
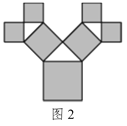
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,設拋物線C1:![]() 的準線1與x軸交于橢圓C2:
的準線1與x軸交于橢圓C2:![]() 的右焦點F2,F1為C2的左焦點.橢圓的離心率為
的右焦點F2,F1為C2的左焦點.橢圓的離心率為![]() ,拋物線C1與橢圓C2交于x軸上方一點P,連接PF1并延長其交C1于點Q,M為C1上一動點,且在P,Q之間移動.
,拋物線C1與橢圓C2交于x軸上方一點P,連接PF1并延長其交C1于點Q,M為C1上一動點,且在P,Q之間移動.

(1)當![]() 取最小值時,求C1和C2的方程;
取最小值時,求C1和C2的方程;
(2)若△PF1F2的邊長恰好是三個連續的自然數,當△MPQ面積取最大值時,求面積最大值以及此時直線MP的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在中國決勝全面建成小康社會的關鍵之年,如何更好地保障和改善民生,如何切實增強政策“獲得感”,成為2019年全國兩會的重要關切.某地區為改善民生調研了甲、乙、丙、丁、戊5個民生項目,得到如下信息:
①若該地區引進甲項目,就必須引進與之配套的乙項目;
②丁、戊兩個項目與民生密切相關,這兩個項目至少要引進一個;
③乙、丙兩個項目之間有沖突,兩個項目只能引進一個;
④丙、丁兩個項目關聯度較高,要么同時引進,要么都不引進;
⑤若引進項目戊,甲、丁兩個項目也必須引進.
則該地區應引進的項目為______.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com