
【題目】![]() =(3
=(3 ![]() sinx,
sinx, ![]() cosx),
cosx), ![]() =(cosx,
=(cosx, ![]() cosx),f (x)=
cosx),f (x)= ![]()
![]() .
.
(1)求f(x)的單調遞減區間;
(2)x∈[﹣ ![]() ,
, ![]() ]時,g(x)=f(x)+m的最大值為
]時,g(x)=f(x)+m的最大值為 ![]() ,求g(x)的最小值及相應的x值.
,求g(x)的最小值及相應的x值.
【答案】
(1)解: ![]() =(3
=(3 ![]() sinx,
sinx, ![]() cosx),
cosx), ![]() =(cosx,
=(cosx, ![]() cosx),
cosx),
∴f (x)= ![]()
![]()
=3 ![]() sinxcosx+3cos2x
sinxcosx+3cos2x
= ![]() sin2x+
sin2x+ ![]()
=3sin(2x+ ![]() )+
)+ ![]() ;
;
令 ![]() +2kπ≤2x+
+2kπ≤2x+ ![]() ≤
≤ ![]() +2kπ,k∈Z,
+2kπ,k∈Z,
解得 ![]() +kπ≤x≤
+kπ≤x≤ ![]() +kπ,k∈Z,
+kπ,k∈Z,
∴f(x)的單調遞減區間是[ ![]() +kπ,
+kπ, ![]() +kπ],k∈Z
+kπ],k∈Z
(2)解:x∈[﹣ ![]() ,
, ![]() ]時,2x+
]時,2x+ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],
],
sin(2x+ ![]() )∈[﹣1,1],
)∈[﹣1,1],
∴3sin(2x+ ![]() )+
)+ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ];
];
∴f(x)的值域是[﹣ ![]() ,
, ![]() ],
],
∴g(x)=f(x)+m的最大值為 ![]() +m=
+m= ![]() ,
,
解得m=1,
∴g(x)=f(x)+1;
∴g(x)的最小值為﹣ ![]() +1=﹣
+1=﹣ ![]() ,
,
此時x=﹣ ![]() .
.
【解析】(1)根據平面向量的數量積計算并化簡f (x),求出f(x)的單調遞減區間;(2)根據x的取值范圍,求出f(x)的值域,再根據g(x)的最大值求出m,從而求出g(x)的最小值與對應x的值.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2cosxsin(x+ ![]() )﹣
)﹣ ![]() sin2x+sinxcosx.
sin2x+sinxcosx.
(1)當x∈[0, ![]() ]時,求f(x)的值域;
]時,求f(x)的值域;
(2)用五點法在圖中作出y=f(x)在閉區間[﹣ ![]() ,
, ![]() ]上的簡圖;
]上的簡圖;
(3)說明f(x)的圖象可由y=sinx的圖象經過怎樣的變化得到? 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,已知R(x0 , y0)是橢圓 ![]() +
+ ![]() =1上的一點,從原點O向圓R(x﹣x0)2+(y﹣y0)2=12作兩條切線,分別交橢圓于P,Q兩點.
=1上的一點,從原點O向圓R(x﹣x0)2+(y﹣y0)2=12作兩條切線,分別交橢圓于P,Q兩點. 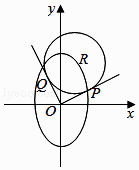
(1)若R點在第一象限,且直線OP,OQ互相垂直,求圓R的方程;
(2)若直線OP,OQ的斜率存在,分別記為k1 , k2 , 求k1k2的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】矩形區域 ABCD 中,AB 長為 2 千米,BC 長為 1 千米,在 A 點和 C 點處各有一個通信基站,其覆蓋范圍均為方圓 1 千米,若在該矩形區域內隨意選取一地點,則該地點無信號的概率為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓M:x2+(y﹣4)2=4,點P是直線l:x﹣2y=0上的一動點,過點P作圓M的切線PA,PB,切點為A,B.
(1)當切線PA的長度為 ![]() 時,求點P的坐標;
時,求點P的坐標;
(2)若△PAM的外接圓為圓N,試問:當P在直線l上運動時,圓N是否過定點?若存在,求出所有的定點的坐標;若不存在,說明理由.
(3)求線段AB長度的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() 其中M∪P=R,則下列結論中一定正確的是( )
其中M∪P=R,則下列結論中一定正確的是( )
A.函數f(x)一定存在最大值
B.函數f(x)一定存在最小值
C.函數f(x)一定不存在最大值
D.函數f(x)一定不存在最小值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,點A(﹣ ![]() ,0),B(
,0),B( ![]() ,0),銳角α的終邊與單位圓O交于點P.
,0),銳角α的終邊與單位圓O交于點P. 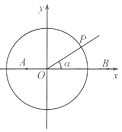
(Ⅰ)用α的三角函數表示點P的坐標;
(Ⅱ)當 ![]()
![]() =﹣
=﹣ ![]() 時,求α的值;
時,求α的值;
(Ⅲ)在x軸上是否存在定點M,使得| ![]() |=
|= ![]() |
| ![]() |恒成立?若存在,求出點M的橫坐標;若不存在,請說明理由.
|恒成立?若存在,求出點M的橫坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正方形ABCD邊長為1,從某時刻起,將線段AB,BC,CD,DA分別繞點A,B,C,D順時針旋轉相同角度α(0<α< ![]() ),若旋轉后的四條線段所圍成的封閉圖形面積為
),若旋轉后的四條線段所圍成的封閉圖形面積為 ![]() ,則α=( )
,則α=( ) 
A.![]() 或
或 ![]()
B.![]() 或
或 ![]()
C.![]() 或
或 ![]()
D.![]() 或
或 ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com